Frecuencia absoluta de un suceso

Imagina que tiramos un dado $100$ veces, y obtenemos un $6$ en $24$ ocasiones. 

En ese caso decimos que la frecuencia absoluta de ese suceso es $24$.

De forma general podríamos definir la frecuencia absoluta de un determinado suceso $A$, de un experimento aleatorio, al número de veces que ocurre el suceso a repetir el experimento $N$ veces.

Para poder comprender mejor este concepto, interactúa con el siguiente applet de Geogebra.

Frecuencia relativa de un suceso

Imagina que tiramos un dado $100$ veces, y obtenemos un $6$ en $24$ ocasiones. 

En ese caso decimos que la frecuencia absoluta de ese suceso es $24$.

A partir de la frecuencia absoluta, podemos definir la frecuencia relativa, que no es más que dividir la frecuencia absoluta entre el número total de veces que hemos repetido el experimento. 

De esta forma, la frecuencia relativa es: $\dfrac{24}{100}=0,24$

De forma general podríamos definir la frecuencia relativa como: $\dfrac{Frecuencia\;absoluta}{N}$

Definimos probabilidad de un suceso $A$, al valor al que se acerca la frecuencia relativa cuando repetimos el suceso muchas veces. Se representa por $P(A)$.

De la definición de frecuencia relativa, podemos deducir que la probabilidad de un suceso siempre está entre $0$ y $1$, es decir:

$0\leq P(A) \leq1$. 

Se verifica:

• La probabilidad del suceso seguro es 1.
• La probabilidad del suceso imposible es cero.  \( P(\emptyset)=0\)
• La probabilidad del suceso contrario es: \(P(\overline{A})=1-P(A)\)
   

Para poder comprender mejor estos conceptos, interactúa con el siguiente applet de Geogebra.

Ley de los grandes números

Utilizando el concepto de frecuencia relativa de un suceso, podemos abordar el estudio de lo que se conoce como Ley de los grandes números.

Lo que nos dice esta ley es que al repetir muchas veces un experimento aleatorio, la frecuencia relativa de un suceso tiende a estabilizarse en un valor constante.

Definimos la probabilidad de un suceso al valor en el que se estabiliza la frecuencia relativa del mismo, al repetir el experimento un número elevado de veces.

Por ejemplo, si tiramos una moneda al aire $200$ veces, y vamos anotando los resultados, observaremos que aproximadamente la frecuencia relativa del suceso "obtener cara" es $0,5$.

Por tanto diremos que la probabilidad del suceso "obtener cara" al tirar una moneda es de $0,5$.

Sucesos equiprobables

Dos sucesos son equiprobables cuando tienen la misma probabilidad de ocurrir.

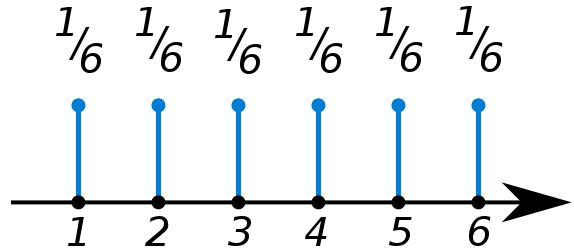
 Por ejemplo, al lanzar un dado normal,

los sucesos posibles son: $\{1\},\{2\},\{3\},\{4\},\{5\},\{6\}$ y tal y como hemos visto,

todos tienen la misma probabilidad de ocurrir.

Decimos que son sucesos equiprobables.

Sin embargo, en el suceso "sacar número par"; $E=\{2\},\{4\},\{6\}$ y el suceso sacar "múltiplo de tres"; $E=\{3\},\{6\}$, no son equiprobables.

El suceso "sacar múltiplo de tres" es más probable que el suceso "número par".

Regla de Laplace

Cuando en un experimento aleatorio todos los sucesos elementales son equiprobables, decimos que es un experimento regular.

La probabilidad en este tipo de sucesos se calcula mediante la Regla de Laplace.

$P (suceso)=\dfrac{Casos\;favorables}{Casos\;posibles}$

Te quedará más claro con un ejemplo:

En la siguiente urna tenemos nueve bolas de colores.

 La probabilidad de extraer una bola de uno de los colores es: 

 $P(V)=\dfrac{3}{9}=0,33$ ya que hay un tres bolas verdes de un total de nueve bolas.

$P(R)=\dfrac{2}{9}=0,22$  ya que hay dos bolas rojas de un total de nueve bolas.

                            $P(A)=\dfrac{4}{9}=0,44$  ya que hay cuatro bolas azules de un total de nueve bolas.