Saltar la navegación

4.4. Prediciendo con las rectas de regresión

Diccionario

Coeficientes

La imagen muestra una expresión algebraica.

Definición:

Valor numérico que multiplica a una variable o incógnita. Indica el número el número de veces que este se repite.

Ejemplo:

El número 3 es el coeficiente en la expresión algebraica 3y.

Predecir

La imagen muestra a un mago que observa una bola de cristal con un signo de interrogación sobre la bola.

Definición:

Acción de anunciar un hecho futuro.

Ejemplo:

No se cumplió ninguna de sus predicciones.

Don Regresión dice...

Ya estamos llegando al final, pero antes, y haciendo honor a mi nombre, me gustaría enseñaros las rectas de regresión, y todo lo que necesitamos saber para poderlas calcular. Te enseñaré a interpretar el valor de los coeficientes y cómo podrás predecir valores de una variable, a partir de un valor dado de la otra variable, todo ello,  haciendo uso de la recta de regresión. 

No es una tarea fácil, pero si has llegado hasta aquí, ya verás como podemos con esto, además será de gran utilidad para tu estudio estadístico deportivo.

Mis nietos te apoyarán en todo momento y harán más fácil esto de la regresión. 

La imagen muestra una expresión algebraica. Definición:

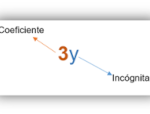
Valor numérico que multiplica a una variable o incógnita. Indica el número el número de veces que este se repite.

Ejemplo:

El número 3 es el coeficiente en la expresión algebraica 3y.

La imagen muestra a un mago que observa una bola de cristal con un signo de interrogación sobre la bola. Definición:

Acción de anunciar un hecho futuro.

Ejemplo:

No se cumplió ninguna de sus predicciones.

Lectura facilitada

Ya estás llegando al final.

Ahora vas a aprender:

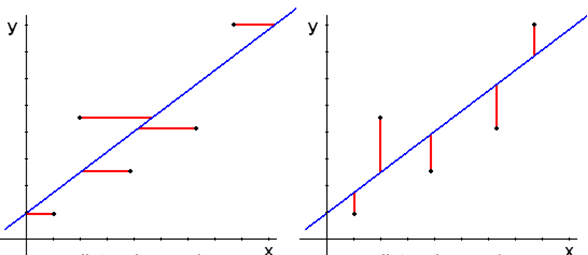
  • Las rectas de regresión.
  • Calcular rectas de regresión. 
  • Interpretar el valor de los coeficientes. 
  • Predecir valores de una variable utilizando la recta de regresión. 

Todo lo aprendido te será de gran utilidad 

para tu estudio estadístico deportivo.

Ajustina y Ajustino te ayudarán en el aprendizaje de las rectas de regresión. 

La imagen muestra una expresión algebraica.

Definición:

Valor numérico que multiplica a una variable o incógnita. Indica el número el número de veces que este se repite.

Ejemplo:

El número 3 es el coeficiente en la expresión algebraica 3y.

La imagen muestra a un mago que observa una bola de cristal con un signo de interrogación sobre la bola.

Definición:

Acción de anunciar un hecho futuro.

Ejemplo:

No se cumplió ninguna de sus predicciones.

1. ¿Calculamos la covarianza?

Ajustino dice...

Empezamos viendo lo que es el centro de gravedad y la covarianza de una distribución bidimensional, luego te voy a enseñar a calcularlos. 

El centro de gravedad de la distribución bidimensional, (X,Y),  es el punto  que tiene como coordenadas las medias de las dos variables.

Centro\ de\ Gravedad\ =(\bar{x},\bar{y})

La Covarianza de la distribución bidimensional, (X,Y),  es una medida que nos permite saber si la relación entre ambas variables es directa o inversa. Se le conoce también como varianza conjunta y se nota y calcula:

\sigma_{xy}=\dfrac{\sum_{i=1}^{n}x_{i}y_{i}f_{i}}{n}-\bar{x}\bar{y}

Si la correlación es positiva, la covarianza es positiva, y si la correlación es negativa, la covarianza es negativa.

Sin embargo, la covarianza no es una buena medida de la correlación, ya que su valor depende de las unidades de las variables, y los valores más alejados del centro de gravedad influyen excesivamente en su valor. Por ello, trabajaremos con el coeficiente de correlación lineal o de Pearson, que te explicará mi hermana después. 

Lectura facilitada

Ahora vas a ver:

  • El centro de gravedad.
  • La covarianza de una distribución bidimensional.

El centro de gravedad de la distribución bidimensional (X,Y) es el punto 

que tiene como coordenadas las medias de las dos variables.

Centro\ de\ Gravedad\ =(\bar{x},\bar{y})

La Covarianza de la distribución bidimensional (X,Y) es una medida 

que te permite saber si la relación entre ambas variables es directa o inversa. 

Se le conoce también como varianza conjunta.

Se nota y se calcula:

\sigma_{xy}=\dfrac{\sum_{i=1}^{n}x_{i}y_{i}f_{i}}{n}-\bar{x}\bar{y}

  • La covarianza es positiva si la correlación es positiva. 
  • La covarianza es negativa si la correlación es negativa. 

La covarianza no es una buena medida de la correlación por:

  • Su valor depende de las unidades de las variables.
  • Los valores más alejados del centro de gravedad influyen en su valor. 

Por ello trabajarás con el coeficiente de correlación lineal o de Pearson. 

Cálculo del centro de gravedad y de la covarianza.

Calculo el centro de gravedad y la covarianza

Paso 1

En la siguiente tabla simple se recogen los pesos y alturas de 20 alumnos y alumnas de 4º de ESO. 

La imagen muestra la tabla de los alumnos

Calculamos tres nuevas filas. 

  • En la primera fila, calcularemos el producto de cada uno de los valores de la variable X por su frecuencia absoluta. 
  • En la segunda fila, calcularemos el producto de cada uno de los valores de la variable Y por su frecuencia absoluta. 
  • Y en la última fila, calcularemos el producto de los valores de ambas variables por su frecuencia absoluta.

La imagen muestra una tabla con los datos del enunciado

Paso 2

Obtenemos el centro de gravedad. Primero calculamos la media de la variable X:

\bar{x}=\dfrac{\sum_{i=1}^{n}x_{i}f_{i}}{n}=\dfrac{1540}{20}=77

A continuación, calculamos la media de la variable Y:

\bar{y}=\dfrac{\sum_{i=1}^{n}y_{i}f_{i}}{n}=\dfrac{34,28}{20}=1.714

Paso 3

Calculamos la covarianza aplicando la fórmula anterior y observamos que es positiva, por tanto, la correlación será positiva (a más peso, más altura).

\sigma_{xy}=\dfrac{\sum_{i=1}^{n}x_{i}y_{i}f_{i}}{n}-\bar{x}\bar{y}=\dfrac{264,24}{20}-77\cdot{1,714}=0,134

2. Coeficiente de correlación lineal o de Pearson

Ajustina dice...

Hemos visto, anteriormente, el concepto de correlación entre dos variables observando la dispersión de la nube de puntos. Para obtener una medida cuantitativa de la correlación entre dos variables necesitamos una fórmula que sirva para obtener su valor de forma numérica e inequívoca. Para ello se utiliza el coeficiente de correlación lineal o de Pearson.

El coeficiente de correlación lineal o de Pearson no va a depender de las unidades y nos va a dar el grado de intensidad de la relación lineal entre las dos variables. Se obtiene:

r\ =\dfrac{\sigma_{xy}}{\sigma_{x}\sigma_{y}}

El coeficiente de correlación lineal tiene un valor comprendido entre -1 y 1.

La imagen muestra una infografía sobre el coeficiente de Pearson

Otro coeficiente que se puede calcular y que resulta muy útil, es el coeficiente de determinación. Para obtenerlo, se eleva al cuadrado el coeficiente de correlación. Este nuevo coeficiente nos va a indicar la parte de variación de la variable dependiente que es explicada por la variable independiente.

¡Vamos a por nuestro ejemplo!

Paso 1

Seguimos con nuestro ejemplo de los pesos y las alturas de un grupo de 20 alumnos de 4º de ESO.

La imagen muestra una tabla con datos de los alumnos

Paso 2

Ya habíamos calculado el centro de gravedad y la covarianza.

Ahora, tendremos que calcular las desviaciones típicas de cada una de las variables estadísticas, de la X y la Y. 

Para ello completamos la tabla que teníamos con dos nuevas filas. 

  • En una fila multiplicamos los valores, al cuadrado, de la variable X por la frecuencia absoluta.

  • En la otra fila, multiplicamos los valores, al cuadrado, de la variable Y por la frecuencia absoluta.

La imagen muestra la tabla de los datos de los alumnos con la desviación típica calculada

Paso 3

Calculamos la desviación de la variable X:

\sigma_{x}^{2}=\dfrac{\sum_{i=1}^{n}x_{i}^{2}f_{i}}{n}-\bar{x}^{2}=\dfrac{118770}{20}-77^{2}=9,498724\longrightarrow\sigma_{x}=3,082

Calculamos la desviación de la variable Y:

\sigma_{y}^{2}=\dfrac{\sum_{i=1}^{n}y_{i}^{2}f_{i}}{n}-\bar{y}^{2}=\dfrac{58,7996}{20}-1,714^{2}=0,00218\longrightarrow\sigma_{y}=0,0467

Paso 4

Finalmente, calculamos el coeficiente de correlación lineal o de Pearson:

r=\dfrac{\sigma_{xy}}{\sigma_{x}\sigma_{y}}=\dfrac{0,134}{3,082\cdot {0,0467}}=0,93

Por ser positivo y próximo a uno, habrá una correlación positiva fuerte. 

Calculamos el coeficiente de determinación:

r^{2}=0.8654

Quiere decir que el 86% de la variable dependiente queda explicado por la independiente.

3. Regresión lineal

Ajustino dice...

Esta es la parte favorita de mi abuelo, ¿te imaginas por qué?

Sí, estudiaremos la regresión lineal.

Cuando tenemos una nube de puntos de una variable estadística bidimensional, podremos intentar trazar una recta que se aproxime, de la mejor forma posible, a los puntos de la nube, es decir, se trata de sustituir la nube de puntos por una recta de manera que, podamos, gracias a la ecuación de la recta, conocido un valor de una de las variables, estimar el valor de la otra variable. A la recta obtenida se le denomina recta de regresión.

La función que mejor se aproxime a la nube de puntos no tiene por qué ser una recta, puede ser otra función: exponencial, logarítmica, … Pero nosotros nos centraremos en la regresión lineal, es decir, calcularemos la recta que mejor se aproxime a la nube de puntos.

Lectura facilitada

Ahora estudiarás la regresión lineal.

Tienes una nube de puntos de una variable estadística bidimensional.

Traza una recta que se aproxime a los puntos de la nube.

Sustituye la nube de puntos por una recta.

Utiliza la ecuación de la recta y estima el valor de la otra variable. 

A la recta obtenida se le denomina recta de regresión.

Método de mínimos cuadrados

Para calcular las rectas de regresión se utiliza el método de los mínimos cuadrados. Consiste en minimizar la distancia entre las ordenadas o las abscisas, es decir, se trata de hallar la recta que cumple que la suma de los cuadrados de las distancias de los puntos de la nube a la recta es mínima, tomando como distancia la diferencia entre la ordenada (abscisa) del punto y la ordenada (abscisa) correspondiente de la recta. Así se obtiene la recta de regresión de Y sobre X (o la de X sobre Y). Es decir, hacemos mínima la suma de las longitudes al cuadrado, de los segmentos rojos del dibujo; según minimicemos los segmentos rojos horizontales o los verticales, tendremos la recta de regresión de X sobre Y o la de Y sobre X. 

La imagen muestra los mínimos cuadrados

Lectura facilitada

Para calcular las rectas de regresión se utiliza el método de los mínimos cuadrados. 

Se trata de hallar la recta que cumple que:

La suma de los cuadrados de las distancias de los puntos de la nube a la recta 

es mínima. 

Toma como distancia la diferencia entre la ordenada que es la abscisa del punto y 

la ordenada correspondiente de la recta. 

Así se obtiene la recta de regresión de Y sobre X.

Así se obtiene la recta de regresión de X sobre Y. 

Haz mínima la suma de las longitudes al cuadrado de los segmentos rojos del dibujo.  

  • Si minimizas los segmentos rojos horizontales tendrás la recta de regresión de X sobre Y.
  • Si minimizas los segmentos rojos verticales tendrás la recta de regresión de Y sobre X. 

La imagen muestra los mínimos cuadrados

La recta de regresión de X sobre Y es (conocemos un valor de la variable Y y queremos calcular el correspondiente valor de la variable X) : 

x-\bar{x}=\dfrac{\sigma_{xy}}{\sigma_{y}^{2}}\ (y-\bar{y})

La recta de regresión de Y sobre X es (conocemos un valor de la variable X y queremos calcular el correspondiente valor de la variable Y) : 

(y-\bar{y})=\dfrac{\sigma_{xy}}{\sigma_{x}^{2}}(x-\bar{x})

Como se puede apreciar, las dos rectas de regresión se cortan en el centro de gravedad, salvo que el coeficiente de correlación lineal sea 1 ó -1, en cuyo caso ambas rectas coinciden.

Las rectas de regresión nos permiten, conocidos los valores de una de las variables, hacer previsiones o estimar de manera aproximada los valores esperados de la otra variable.

Lectura facilitada

La recta de regresión de X sobre Y. 

  • Conoces un valor de la variable Y.
  • Calcula el correspondiente valor de la variable X. 

x-\bar{x}=\dfrac{\sigma_{xy}}{\sigma_{y}^{2}}\ (y-\bar{y})

La recta de regresión de Y sobre X. 

  • Conoces un valor de la variable X. 
  • Calcula el correspondiente valor de la variable Y. 

(y-\bar{y})=\dfrac{\sigma_{xy}}{\sigma_{x}^{2}}(x-\bar{x})

Las dos rectas de regresión se cortan en el centro de gravedad.

Las dos rectas de regresión coinciden si el coeficiente de correlación lineal es 1 ó -1.

Las rectas de regresión te permiten: 

Si conoces los valores de una de las variables

estimar de manera aproximada los valores de la otra variable. 

Con el ejemplo lo comprenderemos mejor

Paso 1

En nuestro ejemplo de los pesos y las alturas, queremos calcular lo siguiente:

  1.   Si el peso es de 74 ¿Qué altura le corresponderá? ¿Es significativo?
  2.   Si la altura es de 1,85cm ¿Qué peso le corresponderá? ¿Es significativo?

La imagen muestra a Ajustino y Ajustina pensando en pesos y alturas

Paso 2

  • Calculamos la recta de regresión de Y sobre X:

y-1,714=\dfrac{0,134}{3,082^{2}}(x-77)

  • A continuación, sustituimos 74 en el valor de x y obtenemos el correspondiente valor de y:

y-1,714=\dfrac{0,134}{3,082^{2}}(74-77)\longrightarrow\ despejando\ y=1,67

Al ser r próximo a 1, el valor obtenido será significativo.

Paso 3

  • Ahora nos toca calcular la recta de regresión de X sobre Y:

x-77=\dfrac{0,134}{0,0467^{2}}(y-1,714)

  • Sustituimos el valor que nos dan en la y, para obtener el correspondiente valor de la x:

x-77=\dfrac{0,134}{0,0467^{2}}(1,85-1,714)\longrightarrow\ despejando\ x=85,36

En este caso no es significativo por haber extrapolado, es decir, haber considerado un valor fuera del intervalo de alturas que nos dan. Por lo tanto, y aunque el r sea próximo a 1, en este caso no será significativo.

4. ¡A calcular rectas de regresión!

Ajustina dice...

Vamos a practicar todo lo aprendido.

¡Comenzamos nuestro entrenamiento!

Opción A: El rosco bidimensional

2

Completa el rosco de palabras relacionadas con la Estadística Bidimensional. Para ello tendrás que leer las definiciones que aparecen. Ten cuidado, ya que unas veces la letra será la primera letra de la palabra, y otras veces, la letra estará contenida en la palabra. 

%E9%B0%E6%EB%E2%F7%D5%F3%FF%F7%B0%A8%B0%C0%FD%E1%F1%FD%B0%BE%B0%FB%FC%E1%E6%E0%E7%F1%E6%FB%FD%FC%E1%B0%A8%B0%AE%E2%AC%D1%FD%FF%E2%FE%F7%E6%F3%B2%F7%FE%B2%E0%FD%E1%F1%FD%B2%F6%F7%B2%E2%F3%FE%F3%F0%E0%F3%E1%B2%E0%F7%FE%F3%F1%FB%FD%FC%F3%F6%F3%E1%B2%F1%FD%FC%B2%FE%F3%B2%D7%E1%E6%F3%F6%7F%E1%E6%FB%F1%F3%B2%D0%FB%F6%FB%FF%F7%FC%E1%FB%FD%FC%F3%FE%BC%B2%C2%F3%E0%F3%B2%F7%FE%FE%FD%B2%E6%F7%FC%F6%E0s%E1%B2%E3%E7%F7%B2%FE%F7%F7%E0%B2%FE%F3%E1%B2%F6%F7%F4%FB%FC%FB%F1%FB%FD%FC%F7%E1%B2%E3%E7%F7%B2%F3%E2%F3%E0%F7%F1%F7%FC%BC%B2%C6%F7%FC%B2%F1%E7%FB%F6%F3%F6%FD%BE%B2%EB%F3%B2%E3%E7%F7%B2%E7%FC%F3%E1%B2%E4%F7%F1%F7%E1%B2%FE%F3%B2%FE%F7%E6%E0%F3%B2%E1%F7%E0s%B2%FE%F3%B2%E2%E0%FB%FF%F7%E0%F3%B2%FE%F7%E6%E0%F3%B2%F6%F7%B2%FE%F3%B2%E2%F3%FE%F3%F0%E0%F3%BE%B2%EB%B2%FD%E6%E0%F3%E1%B2%E4%F7%F1%F7%E1%BE%B2%FE%F3%B2%FE%F7%E6%E0%F3%B2%F7%E1%E6%F3%E0s%B2%F1%FD%FC%E6%F7%FC%FB%F6%F3%B2%F7%FC%B2%FE%F3%B2%E2%F3%FE%F3%F0%E0%F3%BC2%AE%BD%E2%AC%B0%BE%B0%E6%FB%FF%F7%C1%FA%FD%E5%C1%FD%FE%E7%E6%FB%FD%FC%B0%A8%A7%BE%B0%F6%E7%E0%F3%E6%FB%FD%FC%D5%F3%FF%F7%B0%A8%A1%A2%A7%BE%B0%FC%E7%FF%F0%F7%E0%C6%E7%E0%FC%E1%B0%A8%A3%BE%B0%E1%FA%FD%E5%C1%FD%FE%E7%E6%FB%FD%FC%B0%A8%F4%F3%FE%E1%F7%BE%B0%E1%FA%FD%E5%DF%FB%FC%FB%FF%FB%E8%F7%B0%A8%F4%F3%FE%E1%F7%BE%B0%FB%E6%FB%FC%F7%E0%F3%E0%EB%B0%A8%E9%B0%E1%FA%FD%E5%D1%FE%E7%F7%B0%A8%F4%F3%FE%E1%F7%BE%B0%F1%FE%E7%F7%D5%F3%FF%F7%B0%A8%B0%B0%BE%B0%E2%F7%E0%F1%F7%FC%E6%F3%F5%F7%D1%FE%E7%F7%B0%A8%A6%A2%BE%B0%E1%FA%FD%E5%D1%FD%F6%F7%D3%F1%F1%F7%E1%E1%B0%A8%F4%F3%FE%E1%F7%BE%B0%F1%FD%F6%F7%D3%F1%F1%F7%E1%E1%B0%A8%B0%B0%BE%B0%FF%F7%E1%E1%F3%F5%F7%D1%FD%F6%F7%D3%F1%F1%F7%E1%E1%B0%A8%B0%B0%EF%BE%B0%E5%FD%E0%F6%E1%D5%F3%FF%F7%B0%A8%C9%E9%B0%FE%F7%E6%E6%F7%E0%B0%A8%B0%D3%B0%BE%B0%E5%FD%E0%F6%B0%A8%B0%D3%F0%E1%FD%FE%E7%E6%F3%B0%BE%B0%F6%F7%F4%FB%FC%FB%E6%FB%FD%FC%B0%A8%B0%C6%FB%E2%FD%B2%F6%F7%B2%F4%E0%F7%F1%E7%F7%FC%F1%FB%F3%BC%B0%BE%B0%E6%EB%E2%F7%B0%A8%A2%BE%B0%F3%FE%E6%B0%A8%B0%B0%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%E7%E0%FE%B0%A8%B0%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%EF%BE%E9%B0%FE%F7%E6%E6%F7%E0%B0%A8%B0%D0%B0%BE%B0%E5%FD%E0%F6%B0%A8%B0%D0%FB%F6%FB%FF%F7%FC%E1%FB%FD%FC%F3%FE%B0%BE%B0%F6%F7%F4%FB%FC%FB%E6%FB%FD%FC%B0%A8%B0%D6%FB%E1%E6%E0%FB%F0%E7%F1%FBa%FC%B2%F1%FD%FC%B2%F6%FD%E1%B2%E4%F3%E0%FB%F3%F0%FE%F7%E1%B2%F7%E1%E6%F3%F6%7F%E1%E6%FB%F1%F3%E1%BC%B0%BE%B0%E6%EB%E2%F7%B0%A8%A2%BE%B0%F3%FE%E6%B0%A8%B0%B0%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%E7%E0%FE%B0%A8%B0%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%EF%BE%E9%B0%FE%F7%E6%E6%F7%E0%B0%A8%B0%D1%B0%BE%B0%E5%FD%E0%F6%B0%A8%B0%D1%FD%FC%F6%FB%F1%FB%FD%FC%F3%F6%F3%B0%BE%B0%F6%F7%F4%FB%FC%FB%E6%FB%FD%FC%B0%A8%B0%C6%FB%E2%FD%B2%F6%F7%B2%F6%FB%E1%E6%E0%FB%F0%E7%F1%FBa%FC%BC%B0%BE%B0%E6%EB%E2%F7%B0%A8%A2%BE%B0%F3%FE%E6%B0%A8%B0%B0%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%E7%E0%FE%B0%A8%B0%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%EF%BE%E9%B0%FE%F7%E6%E6%F7%E0%B0%A8%B0%D6%B0%BE%B0%E5%FD%E0%F6%B0%A8%B0%D6%FB%E1%E6%E0%FB%F0%E7%F1%FBa%FC%B0%BE%B0%F6%F7%F4%FB%FC%FB%E6%FB%FD%FC%B0%A8%B0%DE%F3%B2%FF%F3%E0%F5%FB%FC%F3%FE%B2%EB%B2%FE%F3%B2%F1%FD%FC%F6%FB%F1%FB%FD%FC%F3%F6%F3%B2%E1%FD%FC%B2%E7%FC%F3%BC%B2%B0%BE%B0%E6%EB%E2%F7%B0%A8%A2%BE%B0%F3%FE%E6%B0%A8%B0%B0%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%E7%E0%FE%B0%A8%B0%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%EF%BE%E9%B0%FE%F7%E6%E6%F7%E0%B0%A8%B0%D7%B0%BE%B0%E5%FD%E0%F6%B0%A8%B0%D7%E1%E6%F3%F6%7F%E1%E6%FB%F1%F3%B0%BE%B0%F6%F7%F4%FB%FC%FB%E6%FB%FD%FC%B0%A8%B0%C0%F3%FF%F3%B2%F6%F7%B2%FE%F3%E1%B2%DF%F3%E6%F7%FFs%E6%FB%F1%F3%E1%B2%E3%E7%F7%B2%B2%E1%F7%B2%FD%F1%E7%E2%F3%B2%F6%F7%B2%E0%F7%F1%FD%F5%F7%E0%BE%B2%F3%FC%F3%FE%FB%E8%F3%E0%B2%EB%B2%F7%EA%E6%E0%F3%F7%E0%B2%FE%F3%B2%FB%FC%F4%FD%E0%FF%F3%F1%FBa%FC%B2%E0%F7%FE%F7%E4%F3%FC%E6%F7%B2%EB%B2h%E6%FB%FE%B2%F6%F7%B2%E7%FC%B2%F1%FD%FC%F8%E7%FC%E6%FD%B2%F6%F7%B2%F6%F3%E6%FD%E1%BC%B2%B0%BE%B0%E6%EB%E2%F7%B0%A8%A2%BE%B0%F3%FE%E6%B0%A8%B0%B0%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%E7%E0%FE%B0%A8%B0%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%EF%BE%E9%B0%FE%F7%E6%E6%F7%E0%B0%A8%B0%D4%B0%BE%B0%E5%FD%E0%F6%B0%A8%B0%D4%E0%F7%F1%E7%F7%FC%F1%FB%F3%B0%BE%B0%F6%F7%F4%FB%FC%FB%E6%FB%FD%FC%B0%A8%B0%DCh%FF%F7%E0%FD%B2%F6%F7%B2%E4%F7%F1%F7%E1%B2%E3%E7%F7%B2%E1%F7%B2%E0%F7%E2%FB%E6%F7%B2%E7%FC%F3%B2%FF%FD%F6%F3%FE%FB%F6%F3%F6%B2%FD%B2%E4%F3%FE%FD%E0%BC%B0%BE%B0%E6%EB%E2%F7%B0%A8%A2%BE%B0%F3%FE%E6%B0%A8%B0%B0%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%E7%E0%FE%B0%A8%B0%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%EF%BE%E9%B0%FE%F7%E6%E6%F7%E0%B0%A8%B0%D5%B0%BE%B0%E5%FD%E0%F6%B0%A8%B0%D5%E0%F3%E4%F7%F6%F3%F6%B0%BE%B0%F6%F7%F4%FB%FC%FB%E6%FB%FD%FC%B0%A8%B0%C2%E7%FC%E6%FD%B2%F4%FD%E0%FF%F3%F6%FD%B2%E2%FD%E0%B2%FE%F3%E1%B2%FF%F7%F6%FB%F3%E1%B2%F6%F7%B2%FE%F3%E1%B2%F6%FD%E1%B2%E4%F3%E0%FB%F3%F0%FE%F7%E1%B2%F7%E1%E6%F3%F6%7F%E1%E6%FB%F1%F3%E1%BC%B0%BE%B0%E6%EB%E2%F7%B0%A8%A2%BE%B0%F3%FE%E6%B0%A8%B0%B0%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%E7%E0%FE%B0%A8%B0%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%EF%BE%E9%B0%FE%F7%E6%E6%F7%E0%B0%A8%B0%DA%B0%BE%B0%E5%FD%E0%F6%B0%A8%B0%DA%FB%E1%E6%FD%F5%E0%F3%FF%F3%B0%BE%B0%F6%F7%F4%FB%FC%FB%E6%FB%FD%FC%B0%A8%B0%D5%E0s%F4%FB%F1%FD%B2%E2%F3%E0%F3%B2%E0%F7%E2%E0%F7%E1%F7%FC%E6%F3%E0%B2%E4%F3%E0%FB%F3%F0%FE%F7%E1%B2%F7%E1%E6%F3%F6%7F%E1%E6%FB%F1%F3%E1%B2%F1%FD%FC%E6%FB%FC%E7%F3%E1%BC%B0%BE%B0%E6%EB%E2%F7%B0%A8%A2%BE%B0%F3%FE%E6%B0%A8%B0%B0%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%E7%E0%FE%B0%A8%B0%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%EF%BE%E9%B0%FE%F7%E6%E6%F7%E0%B0%A8%B0%DB%B0%BE%B0%E5%FD%E0%F6%B0%A8%B0%DB%FC%F6%FB%E4%FB%F6%E7%FD%B0%BE%B0%F6%F7%F4%FB%FC%FB%E6%FB%FD%FC%B0%A8%B0%D1%F3%F6%F3%B2%E7%FC%F3%B2%F6%F7%B2%FE%F3%E1%B2%E7%FC%FB%F6%F3%F6%F7%E1%B2%F7%FE%F7%FF%F7%FC%E6%F3%FE%F7%E1%B2%E3%E7%F7%B2%F4%FD%E0%FF%F3%FC%B2%FE%F3%B2%E2%FD%F0%FE%F3%F1%FBa%FC%BC%B0%BE%B0%E6%EB%E2%F7%B0%A8%A2%BE%B0%F3%FE%E6%B0%A8%B0%B0%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%E7%E0%FE%B0%A8%B0%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%EF%BE%E9%B0%FE%F7%E6%E6%F7%E0%B0%A8%B0%D8%B0%BE%B0%E5%FD%E0%F6%B0%A8%B0%C2%FD%E0%F1%F7%FC%E6%F3%F8%F7%B0%BE%B0%F6%F7%F4%FB%FC%FB%E6%FB%FD%FC%B0%A8%B0%C1%F7%B2%FD%F0%E6%FB%F7%FC%F7%B2%FF%E7%FE%E6%FB%E2%FE%FB%F1%F3%FC%F6%FD%B2%E2%FD%E0%B2%A3%A2%A2%B2%FE%F3%B2%F4%E0%F7%F1%E7%F7%FC%F1%FB%F3%B2%E0%F7%FE%F3%E6%FB%E4%F3%BC%B0%BE%B0%E6%EB%E2%F7%B0%A8%A3%BE%B0%F3%FE%E6%B0%A8%B0%B0%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%E7%E0%FE%B0%A8%B0%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%EF%BE%E9%B0%FE%F7%E6%E6%F7%E0%B0%A8%B0%D9%B0%BE%B0%E5%FD%E0%F6%B0%A8%B0%D9%F3%E0%FE%B0%BE%B0%F6%F7%F4%FB%FC%FB%E6%FB%FD%FC%B0%A8%B0%DC%FD%FF%F0%E0%F7%B2%E2%E0%FD%E2%FB%FD%B2%F6%F7%B2%E7%FC%B2%FF%F3%E6%F7%FFs%E6%FB%F1%FD%B2%E3%E7%F7%B2%F6%F7%E1%E6%F3%F1a%B2%F7%FC%B2%D7%E1%E6%F3%F6%7F%E1%E6%FB%F1%F3%B2%EB%B2%E6%FB%F7%FC%F7%B2%E7%FC%B2%F1%FD%F7%F4%FB%F1%FB%F7%FC%E6%F7%BC%B0%BE%B0%E6%EB%E2%F7%B0%A8%A2%BE%B0%F3%FE%E6%B0%A8%B0%B0%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%E7%E0%FE%B0%A8%B0%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%EF%BE%E9%B0%FE%F7%E6%E6%F7%E0%B0%A8%B0%DE%B0%BE%B0%E5%FD%E0%F6%B0%A8%B0%DE%FB%FC%F7%F3%FE%B0%BE%B0%F6%F7%F4%FB%FC%FB%E6%FB%FD%FC%B0%A8%B0%C6%FB%E2%FD%B2%F6%F7%B2%E0%F7%F5%E0%F7%E1%FBa%FC%BC%B0%BE%B0%E6%EB%E2%F7%B0%A8%A2%BE%B0%F3%FE%E6%B0%A8%B0%B0%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%E7%E0%FE%B0%A8%B0%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%EF%BE%E9%B0%FE%F7%E6%E6%F7%E0%B0%A8%B0%DF%B0%BE%B0%E5%FD%E0%F6%B0%A8%B0%DF%F3%E0%F5%FB%FC%F3%FE%B0%BE%B0%F6%F7%F4%FB%FC%FB%E6%FB%FD%FC%B0%A8%B0%C6%FB%E2%FD%B2%F6%F7%B2%F6%FB%E1%E6%E0%FB%F0%E7%F1%FBa%FC%BC%B0%BE%B0%E6%EB%E2%F7%B0%A8%A2%BE%B0%F3%FE%E6%B0%A8%B0%B0%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%E7%E0%FE%B0%A8%B0%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%EF%BE%E9%B0%FE%F7%E6%E6%F7%E0%B0%A8%B0%DC%B0%BE%B0%E5%FD%E0%F6%B0%A8%B0%DC%E7%F0%F7%B0%BE%B0%F6%F7%F4%FB%FC%FB%E6%FB%FD%FC%B0%A8%B0%D6%FB%F3%F5%E0%F3%FF%F3%B2%E2%F3%E0%F3%B2%E0%F7%E2%E0%F7%E1%F7%FC%E6%F3%E0%B2%FE%F3%E1%B2%E4%F3%E0%FB%F3%F0%FE%F7%E1%B2%F7%E1%E6%F3%F6%7F%E1%E6%FB%F1%F3%E1%B2%F0%FB%F6%FB%FF%F7%FC%E1%FB%FD%FC%F3%FE%F7%E1%B0%BE%B0%E6%EB%E2%F7%B0%A8%A2%BE%B0%F3%FE%E6%B0%A8%B0%B0%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%E7%E0%FE%B0%A8%B0%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%EF%BE%E9%B0%FE%F7%E6%E6%F7%E0%B0%A8%B0C%B0%BE%B0%E5%FD%E0%F6%B0%A8%B0%B0%BE%B0%F6%F7%F4%FB%FC%FB%E6%FB%FD%FC%B0%A8%B0%B0%BE%B0%E6%EB%E2%F7%B0%A8%A2%BE%B0%F3%FE%E6%B0%A8%B0%B0%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%E7%E0%FE%B0%A8%B0%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%EF%BE%E9%B0%FE%F7%E6%E6%F7%E0%B0%A8%B0%DD%B0%BE%B0%E5%FD%E0%F6%B0%A8%B0%D1%FD%E0%E0%F7%FE%F3%F1%FBa%FC%B0%BE%B0%F6%F7%F4%FB%FC%FB%E6%FB%FD%FC%B0%A8%B0%C6%FB%E2%FD%B2%EB%B2%F5%E0%F3%F6%FD%B2%F6%F7%B2%E0%F7%FE%F3%F1%FBa%FC%B2%FD%B2%F6%F7%E2%F7%FC%F6%F7%FC%F1%FB%F3%B2%F7%FC%E6%E0%F7%B2%F3%FF%F0%F3%E1%B2%E4%F3%E0%FB%F3%F0%FE%F7%E1%BC%B0%BE%B0%E6%EB%E2%F7%B0%A8%A3%BE%B0%F3%FE%E6%B0%A8%B0%B0%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%E7%E0%FE%B0%A8%B0%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%EF%BE%E9%B0%FE%F7%E6%E6%F7%E0%B0%A8%B0%C2%B0%BE%B0%E5%FD%E0%F6%B0%A8%B0%C2%FD%FE%7F%F5%FD%FC%FD%B0%BE%B0%F6%F7%F4%FB%FC%FB%E6%FB%FD%FC%B0%A8%B0%D5%E0s%F4%FB%F1%FD%B2%E2%F3%E0%F3%B2%E0%F7%E2%E0%F7%E1%F7%FC%E6%F3%E0%B2%E4%F3%E0%FB%F3%F0%FE%F7%E1%B2%F1%E7%F3%FC%E6%FB%E6%F3%E6%FB%E4%F3%E1%BC%B0%BE%B0%E6%EB%E2%F7%B0%A8%A2%BE%B0%F3%FE%E6%B0%A8%B0%B0%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%E7%E0%FE%B0%A8%B0%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%EF%BE%E9%B0%FE%F7%E6%E6%F7%E0%B0%A8%B0%C3%B0%BE%B0%E5%FD%E0%F6%B0%A8%B0%D7%E3%E7%FB%E4%F3%FE%F7%FC%E6%F7%B0%BE%B0%F6%F7%F4%FB%FC%FB%E6%FB%FD%FC%B0%A8%B0%DB%F5%E7%F3%FE%BC%B0%BE%B0%E6%EB%E2%F7%B0%A8%A3%BE%B0%F3%FE%E6%B0%A8%B0%B0%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%E7%E0%FE%B0%A8%B0%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%EF%BE%E9%B0%FE%F7%E6%E6%F7%E0%B0%A8%B0%C0%B0%BE%B0%E5%FD%E0%F6%B0%A8%B0%C0%F7%F5%E0%F7%E1%FBa%FC%B0%BE%B0%F6%F7%F4%FB%FC%FB%E6%FB%FD%FC%B0%A8%B0%C6%FB%E2%FD%B2%F6%F7%B2%E0%F7%F1%E6%F3%B2%E3%E7%F7%B2%E1%F7%B2%E7%E6%FB%FE%FB%E8%F3%B2%E2%F3%E0%F3%B2%F7%E1%E6%FB%FF%F3%E0%B2%F7%FE%B2%E4%F3%FE%FD%E0%B2%F6%F7%B2%E7%FC%F3%B2%E4%F3%E0%FB%F3%F0%FE%F7%BC%B0%BE%B0%E6%EB%E2%F7%B0%A8%A2%BE%B0%F3%FE%E6%B0%A8%B0%B0%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%E7%E0%FE%B0%A8%B0%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%EF%BE%E9%B0%FE%F7%E6%E6%F7%E0%B0%A8%B0%C1%B0%BE%B0%E5%FD%E0%F6%B0%A8%B0%C1%FB%FF%E2%FE%F7%B0%BE%B0%F6%F7%F4%FB%FC%FB%E6%FB%FD%FC%B0%A8%B0%C6%FB%E2%FD%B2%F6%F7%B2%E6%F3%F0%FE%F3%B2%E2%F3%E0%F3%B2%E0%F7%F1%FD%E2%FB%FE%F3%E0%B2%F6%F3%E6%FD%E1%B2%F6%F7%B2%E7%FC%F3%B2%E4%F3%E0%FB%F3%F0%FE%F7%B2%F0%FB%F6%FB%FF%F7%FC%E1%FB%FD%FC%F3%FE%BC%B0%BE%B0%E6%EB%E2%F7%B0%A8%A2%BE%B0%F3%FE%E6%B0%A8%B0%B0%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%E7%E0%FE%B0%A8%B0%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%EF%BE%E9%B0%FE%F7%E6%E6%F7%E0%B0%A8%B0%C6%B0%BE%B0%E5%FD%E0%F6%B0%A8%B0%C6%F3%F0%FE%F3%B0%BE%B0%F6%F7%F4%FB%FC%FB%E6%FB%FD%FC%B0%A8%B0%D6a%FC%F6%F7%B2%E1%F7%B2%E0%F7%F1%FD%F5%F7%FC%B2%FE%F3%E1%B2%F4%E0%F7%F1%E7%F7%FC%F1%FB%F3%E1%BC%B0%BE%B0%E6%EB%E2%F7%B0%A8%A2%BE%B0%F3%FE%E6%B0%A8%B0%B0%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%E7%E0%FE%B0%A8%B0%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%EF%BE%E9%B0%FE%F7%E6%E6%F7%E0%B0%A8%B0%C7%B0%BE%B0%E5%FD%E0%F6%B0%A8%B0%DF%E7%F7%E1%E6%E0%F3%B0%BE%B0%F6%F7%F4%FB%FC%FB%E6%FB%FD%FC%B0%A8%B0%C1%E7%F0%F1%FD%FC%F8%E7%FC%E6%FD%B2%F6%F7%B2%FE%F3%B2%E2%FD%F0%FE%F3%F1%FBa%FC%B2%E1%FD%F0%E0%F7%B2%FE%F3%B2%E3%E7%F7%B2%E1%F7%B2%E0%F7%F3%FE%FB%E8%F3%B2%F7%FE%B2%F7%E1%E6%E7%F6%FB%FD%BC%B0%BE%B0%E6%EB%E2%F7%B0%A8%A3%BE%B0%F3%FE%E6%B0%A8%B0%B0%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%E7%E0%FE%B0%A8%B0%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%EF%BE%E9%B0%FE%F7%E6%E6%F7%E0%B0%A8%B0%C4%B0%BE%B0%E5%FD%E0%F6%B0%A8%B0%C4%F3%E0%FB%F3%FC%E8%F3%B0%BE%B0%F6%F7%F4%FB%FC%FB%E6%FB%FD%FC%B0%A8%B0%DF%F7%F6%FB%F6%F3%B2%F6%F7%B2%F6%FB%E1%E2%F7%E0%E1%FBa%FC%BC%B2%B0%BE%B0%E6%EB%E2%F7%B0%A8%A2%BE%B0%F3%FE%E6%B0%A8%B0%B0%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%E7%E0%FE%B0%A8%B0%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%EF%BE%E9%B0%FE%F7%E6%E6%F7%E0%B0%A8%B0%C5%B0%BE%B0%E5%FD%E0%F6%B0%A8%B0%B0%BE%B0%F6%F7%F4%FB%FC%FB%E6%FB%FD%FC%B0%A8%B0%B0%BE%B0%E6%EB%E2%F7%B0%A8%A2%BE%B0%F3%FE%E6%B0%A8%B0%B0%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%E7%E0%FE%B0%A8%B0%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%EF%BE%E9%B0%FE%F7%E6%E6%F7%E0%B0%A8%B0%CA%B0%BE%B0%E5%FD%E0%F6%B0%A8%B0%D7%EA%E6%E0%F3%E2%FD%FE%F3%E0%B0%BE%B0%F6%F7%F4%FB%FC%FB%E6%FB%FD%FC%B0%A8%B0%D7%E1%E6%FB%FF%F3%E0%B2%E7%FC%B2%E4%F3%FE%FD%E0%B2%E3%E7%F7%B2%F7%E1%E6s%B2%F4%E7%F7%E0%F3%B2%F6%F7%FE%B2%FB%FC%E6%F7%E0%E4%F3%FE%FD%BC%B0%BE%B0%E6%EB%E2%F7%B0%A8%A3%BE%B0%F3%FE%E6%B0%A8%B0%B0%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%E7%E0%FE%B0%A8%B0%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%EF%BE%E9%B0%FE%F7%E6%E6%F7%E0%B0%A8%B0%CB%B0%BE%B0%E5%FD%E0%F6%B0%A8%B0%CB%B0%BE%B0%F6%F7%F4%FB%FC%FB%E6%FB%FD%FC%B0%A8%B0%C1%F7%F5%E7%FC%F6%F3%B2%E4%F3%E0%FB%F3%F0%FE%F7%B2%F6%F7%B2%E7%FC%F3%B2%F6%FB%E1%E6%E0%FB%F0%E7%F1%FBa%FC%B2%F0%FB%F6%FB%FF%F7%FC%E1%FB%FD%FC%F3%FE%BC%B0%BE%B0%E6%EB%E2%F7%B0%A8%A2%BE%B0%F3%FE%E6%B0%A8%B0%B0%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%E7%E0%FE%B0%A8%B0%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%EF%BE%E9%B0%FE%F7%E6%E6%F7%E0%B0%A8%B0%C8%B0%BE%B0%E5%FD%E0%F6%B0%A8%B0%D1%FD%E4%F3%E0%FB%F3%FC%E8%F3%B0%BE%B0%F6%F7%F4%FB%FC%FB%E6%FB%FD%FC%B0%A8%B0%DF%F7%F6%FB%F6%F3%B2%E3%E7%F7%B2%FC%FD%E1%B2%E2%F7%E0%FF%FB%E6%F7%B2%E1%F3%F0%F7%E0%B2%E1%FB%B2%FE%F3%B2%E0%F7%FE%F3%F1%FBa%FC%B2%F7%FC%E6%E0%F7%B2%F3%FF%F0%F3%E1%B2%E4%F3%E0%FB%F3%F0%FE%F7%E1%B2%F7%E1%B2%F6%FB%E0%F7%F1%E6%F3%B2%FD%B2%FB%FC%E4%F7%E0%E1%F3%BC%B2%B0%BE%B0%E6%EB%E2%F7%B0%A8%A3%BE%B0%F3%FE%E6%B0%A8%B0%B0%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%E7%E0%FE%B0%A8%B0%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%EF%CF%BE%B0%FB%E1%C1%F1%FD%E0%FF%B0%A8%A2%BE%B0%E6%F7%EA%E6%D0%E7%E6%E6%FD%FC%C1%F1%FD%E0%FF%B0%A8%B0%D5%E7%F3%E0%F6%F3%E0%B2%FE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B0%BE%B0%E0%F7%E2%F7%F3%E6%D3%F1%E6%FB%E4%FB%E6%EB%B0%A8%F4%F3%FE%E1%F7%BE%B0%FE%F7%E6%E6%F7%E0%E1%B0%A8%B0%D3%D0%D1%D6%D7%D4%D5%DA%DB%D8%D9%DE%DF%DCC%DD%C2%C3%C0%C1%C6%C7%C4%C5%CA%CB%C8%B0%BE%B0%E6%F7%EA%E6%D3%F4%E6%F7%E0%B0%A8%B0%B0%BE%B0%F1%F3%E1%F7%C1%F7%FC%E1%FB%E6%FB%E4%F7%B0%A8%F4%F3%FE%E1%F7%BE%B0%E4%F7%E0%E1%FB%FD%FC%B0%A8%A0%BE%B0%FF%E1%F5%E1%B0%A8%E9%B0%FF%E1%F5%C0%F7%F3%F6%EB%B0%A8%B0-%C2%E0%F7%E2%F3%E0%F3%F6%FD%AD%B0%BE%B0%FF%E1%F5%C1%E6%F3%E0%E6%D5%F3%FF%F7%B0%A8%B0%C2%E7%FE%E1%F7%B2%F3%E3%E7%7F%B2%E2%F3%E0%F3%B2%F7%FF%E2%F7%E8%F3%E0%B0%BE%B0%FF%E1%F5%DA%F3%E2%E2%F7%FC%B0%A8%B0%C2%F3%E1%F3%E0%B0%BE%B0%FF%E1%F5%C0%F7%E2%FE%EB%B0%A8%B0%C0%F7%E1%E2%FD%FC%F6%F7%E0%B0%BE%B0%FF%E1%F5%C1%E7%F0%FF%FB%E6%B0%A8%B0%D7%FC%E4%FB%F3%E0%B0%BE%B0%FF%E1%F5%D7%FC%E6%F7%E0%D1%FD%F6%F7%B0%A8%B0%DB%FC%E6%E0%FD%F6%E7%E8%F1%F3%B2%F7%FE%B2%F1a%F6%FB%F5%FD%B2%F6%F7%B2%F3%F1%F1%F7%E1%FD%B0%BE%B0%FF%E1%F5%D7%E0%E0%FD%E0%D1%FD%F6%F7%B0%A8%B0%D7%FE%B2%F1a%F6%FB%F5%FD%B2%F6%F7%B2%F3%F1%F1%F7%E1%FD%B2%FC%FD%B2%F7%E1%B2%F1%FD%E0%E0%F7%F1%E6%FD%B0%BE%B0%FF%E1%F5%D5%F3%FF%F7%DD%E4%F7%E0%B0%A8%B03%D4%FB%FC%B2%F6%F7%B2%FE%F3%B2%E2%F3%E0%E6%FB%F6%F3%B3%B0%BE%B0%FF%E1%F5%DC%F7%E5%C5%FD%E0%F6%B0%A8%B0%C2%F3%FE%F3%F0%E0%F3%B2%FC%E7%F7%E4%F3%B0%BE%B0%FF%E1%F5%C1%E6%F3%E0%E6%C5%FB%E6%FA%B0%A8%B0%D7%FF%E2%FB%F7%E8%F3%B2%E2%FD%E0%B2%B7%A3%B0%BE%B0%FF%E1%F5%D1%FD%FC%E6%F3%FB%FC%E6%B0%A8%B0%D1%FD%FC%E6%FB%F7%FC%F7%B2%FE%F3%B2%FE%F7%E6%E0%F3%B2%B7%A3%B0%BE%B0%FF%E1%F5%C2%F3%E1%E1%B0%A8%B0%C2%F3%E1%F3%E0%B2%F3%B2%FE%F3%B2%E1%FB%F5%E7%FB%F7%FC%E6%F7%B2%E2%F3%FE%F3%F0%E0%F3%B0%BE%B0%FF%E1%F5%DB%FC%F6%FB%F1%F3%E6%F7%C5%FD%E0%F6%B0%A8%B0%DB%FC%E6%E0%FD%F6%E7%E8%F1%F3%B2%E7%FC%F3%B2%E2%F3%FE%F3%F0%E0%F3%B0%BE%B0%FF%E1%F5%D1%FE%E7%F7%B0%A8%B03%D5%F7%FC%FB%F3%FE%B3%B2%DE%F3%B2%E2%FB%E1%E6%F3%B2%F7%E1%A8%B0%BE%B0%FF%E1%F5%DC%F7%E5%D5%F3%FF%F7%B0%A8%B0%C2%E7%FE%E1%F7%B2%F3%E3%E7%7F%B2%E2%F3%E0%F3%B2%F7%FF%E2%F7%E8%F3%E0%B2%FD%E6%E0%F3%B2%E2%F3%E0%E6%FB%F6%F3%B0%BE%B0%FF%E1%F5%CB%FD%E7%DA%F3%E1%B0%A8%B0%C6%FB%F7%FC%F7%B2%B7%A3%B2%F3%F1%FB%F7%E0%E6%FD%E1%B2%EB%B2%B7%A0%B2%F4%F3%FE%FE%FD%E1%B0%BE%B0%FF%E1%F5%D1%FD%F6%F7%D3%F1%F1%F7%E1%E1%B0%A8%B0%D1a%F6%FB%F5%FD%B2%F6%F7%B2%F3%F1%F1%F7%E1%FD%B0%BE%B0%FF%E1%F5%C2%FE%F3%EB%D3%F5%F3%FB%FC%B0%A8%B0%D8%E7%F5%F3%E0%B2%FD%E6%E0%F3%B2%E4%F7%E8%B0%BE%B0%FF%E1%F5%C0%F7%E3%E7%FB%E0%F7%F6%D3%F1%F1%F7%E1%E1%D9%F7%EB%B0%A8%B0%D7%E1%B2%FC%F7%F1%F7%E1%F3%E0%FB%FD%B2%F7%FE%B2%F1a%F6%FB%F5%FD%B2%F6%F7%B2%F3%F1%F1%F7%E1%FD%B0%BE%B0%FF%E1%F5%DB%FC%F4%FD%E0%FF%F3%E6%FB%FD%FC%DE%FD%FD%F9%FB%FC%F5%B0%A8%B0%DE%F3%B2%FB%FC%F4%FD%E0%FF%F3%F1%FBa%FC%B2%E3%E7%F7%B2%F7%E1%E6%F3%F0%F3%B2%F0%E7%E1%F1%F3%FC%F6%FD%B0%BE%B0%FF%E1%F5%C2%FE%F3%EB%C1%E6%F3%E0%E6%B0%A8%B0%C2%E7%FE%E1%F7%B2%F3%E3%E7%7F%B2%E2%F3%E0%F3%B2%F8%E7%F5%F3%E0%B0%BE%B0%FF%E1%F5%D7%E0%E0%FD%E0%E1%B0%A8%B0%D7%E0%E0%FD%E0%F7%E1%B0%BE%B0%FF%E1%F5%DF%FB%FC%FB%FF%FB%E8%F7%B0%A8%B0%DF%FB%FC%FB%FF%FB%E8%F3%E0%B0%BE%B0%FF%E1%F5%DF%F3%EA%FB%FF%FB%E8%F7%B0%A8%B0%DF%F3%EA%FB%FF%FB%E8%F3%E0%B0%BE%B0%FF%E1%F5%DA%FB%E6%E1%B0%A8%B0%D3%F1%FB%F7%E0%E6%FD%E1%B0%BE%B0%FF%E1%F5%C6%FB%FF%F7%B0%A8%B0%DE%7F%FF%FB%E6%F7%B2%F6%F7%B2%E6%FB%F7%FF%E2%FD%B2%BA%FF%FF%A8%E1%E1%BB%B0%BE%B0%FF%E1%F5%DD%FC%F7%C0%FD%E7%FC%F6%B0%A8%B0%C7%FC%F3%B2%E4%E7%F7%FE%E6%F3%B0%BE%B0%FF%E1%F5%C6%FD%E5%C0%FD%E7%FC%F6%E1%B0%A8%B0%D6%FD%E1%B2%E4%E7%F7%FE%E6%F3%E1%B0%BE%B0%FF%E1%F5%DB%FF%F3%F5%F7%B0%A8%B0%DB%FF%F3%F5%F7%FC%B0%BE%B0%FF%E1%F5%DC%FD%DB%FF%F3%F5%F7%B0%A8%B0%C1%FB%FC%B2%FB%FFs%F5%F7%FC%F7%E1%B0%BE%B0%FF%E1%F5%C5%E0%FD%E6%F7%B0%A8%B0%D7%E1%F1%E0%FB%F0%F3%B2%FE%F3%B2%E2%F3%FE%F3%F0%E0%F3%B2%F1%FD%E0%E0%F7%F1%E6%F3%B2%EB%B2%E2%E7%FE%E1%F7%B2%F7%FC%B2%C0%F7%E1%E2%FD%FC%F6%F7%E0%BC%B2%C1%FB%B2%F6%E7%F6%F3%BE%B2%E2%E7%FE%E1%F7%B2%F7%FC%B2%C1%F7%F5%E7%FB%E0%BC%B0%BE%B0%FF%E1%F5%DC%FD%E6%DC%F7%E6%E5%FD%E0%F9%B0%A8%B0%D3%B2%F7%E1%E6%F7%B2%F8%E7%F7%F5%FD%B2%E1a%FE%FD%B2%E1%F7%B2%E2%E7%F7%F6%F7%B2%F8%E7%F5%F3%E0%B2%F1%FD%FC%B2%F1%FD%FC%F7%EA%FBa%FC%B2%F3%B2%FB%FC%E6%F7%E0%FC%F7%E6%BC%B0%BE%B0%FF%E1%F5%C1%E7%F1%F1%F7%E1%E1%F7%E1%B0%A8%B03%D1%FD%E0%E0%F7%F1%E6%FD%B3%B2%EE%B23%D7%EA%F1%F7%FE%F7%FC%E6%F7%B3%B2%EE%B23%D5%F7%FC%FB%F3%FE%B3%B2%EE%B23%DF%E7%EB%B2%F0%FB%F7%FC%B3%B2%EE%B23%C2%F7%E0%F4%F7%F1%E6%FD%B3%B0%BE%B0%FF%E1%F5%D4%F3%FB%FE%E7%E0%F7%E1%B0%A8%B03%DC%FD%B2%F7%E0%F3%B2%F7%E1%FD%B3%B2%EE%B23%DB%FC%F1%FD%E0%E0%F7%F1%E6%FD%B3%B2%EE%B23%DC%FD%B2%F7%E1%B2%F1%FD%E0%E0%F7%F1%E6%FD%B3%B2%EE%B23%DE%FD%B2%E1%F7%FC%E6%FB%FF%FD%E1%B3%B2%EE%B23%D7%E0%E0%FD%E0%B3%B0%BE%B0%FF%E1%F5%D7%FC%F6%D5%F3%FF%F7%C1%F1%FD%E0%F7%B0%A8%B0%D3%FC%E6%F7%E1%B2%F6%F7%B2%F5%E7%F3%E0%F6%F3%E0%B2%FE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%F1%FD%FF%FB%F7%FC%F1%F7%B2%FE%F3%B2%E2%F3%E0%E6%FB%F6%F3%BC%B0%BE%B0%FF%E1%F5%C1%F1%FD%E0%F7%C1%F1%FD%E0%FF%B0%A8%B0%DE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%FC%FD%B2%E1%F7%B2%E2%E7%F7%F6%F7%B2%F5%E7%F3%E0%F6%F3%E0%B2%E2%FD%E0%E3%E7%F7%B2%F7%E1%E6%F3%B2%E2s%F5%FB%FC%F3%B2%FC%FD%B2%F4%FD%E0%FF%F3%B2%E2%F3%E0%E6%F7%B2%B2%F6%F7%B2%E7%FC%B2%E2%F3%E3%E7%F7%E6%F7%B2%C1%D1%DD%C0%DF%BC%B0%BE%B0%FF%E1%F5%C1%FA%FD%E5%C0%FD%E7%FE%F7%E6%E6%F7%B0%A8%B0%DF%FD%E1%E6%E0%F3%E0%B2%F7%FE%B2%E0%FD%E1%F1%FD%B2%F6%F7%B2%E2%F3%FE%F3%F0%E0%F3%E1%B0%BE%B0%FF%E1%F5%DA%FB%F6%F7%C0%FD%E7%FE%F7%E6%E6%F7%B0%A8%B0%DD%F1%E7%FE%E6%F3%E0%B2%F7%FE%B2%E0%FD%E1%F1%FD%B2%F6%F7%B2%E2%F3%FE%F3%F0%E0%F3%E1%B0%BE%B0%FF%E1%F5%C3%E7%F7%E1%E6%FB%FD%FC%B0%A8%B0%C2%E0%F7%F5%E7%FC%E6%F3%B0%BE%B0%FF%E1%F5%D3%FC%E1%E5%F7%E0%B0%A8%B0%C0%F7%E1%E2%FD%FC%F6%F7%E0%B0%BE%B0%FF%E1%F5%DD%FC%FE%EB%C1%F3%E4%F7%C1%F1%FD%E0%F7%B0%A8%B03%C1a%FE%FD%B2%E2%E7%F7%F6%F7%B2%F5%E7%F3%E0%F6%F3%E0%B2%FE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%E7%FC%F3%B2%E4%F7%E8%B3%B0%BE%B0%FF%E1%F5%DD%FC%FE%EB%C1%F3%E4%F7%B0%A8%B0%C1a%FE%FD%B2%E2%E7%F7%F6%F7%B2%F5%E7%F3%E0%F6%F3%E0%B2%E7%FC%F3%B2%E4%F7%E8%B0%BE%B0%FF%E1%F5%DB%FC%F4%FD%E0%FF%F3%E6%FB%FD%FC%B0%A8%B0%DB%FC%F4%FD%E0%FF%F3%F1%FBa%FC%B0%BE%B0%FF%E1%F5%CB%FD%E7%C1%F1%FD%E0%F7%B0%A8%B0%C1%E7%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B0%BE%B0%FF%E1%F5%DD%FC%FE%EB%C1%F3%E4%F7%D3%E7%E6%FD%B0%A8%B0%C1%E7%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%E1%F7%B2%F5%E7%F3%E0%F6%F3%E0s%B2%F6%F7%E1%E2%E7%7B%E1%B2%F6%F7%B2%F1%F3%F6%F3%B2%E2%E0%F7%F5%E7%FC%E6%F3%BC%B2%C1a%FE%FD%B2%E2%E7%F7%F6%F7%B2%F8%E7%F5%F3%E0%B2%E7%FC%F3%B2%E4%F7%E8%BC%B0%BE%B0%FF%E1%F5%C1%F3%E4%F7%D3%E7%E6%FD%B0%A8%B0%C1%E7%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%E1%F7%B2%F5%E7%F3%E0%F6%F3%E0s%B2%F3%E7%E6%FD%FFs%E6%FB%F1%F3%FF%F7%FC%E6%F7%B2%F6%F7%E1%E2%E7%7B%E1%B2%F6%F7%B2%F1%F3%F6%F3%B2%E2%E0%F7%F5%E7%FC%E6%F3%BC%B0%BE%B0%FF%E1%F5%D3%E7%E6%FA%FD%E0%B0%A8%B0%D3%E7%E6%FD%E0%B0%BE%B0%FF%E1%F5%C1%F7%E4%F7%E0%F3%FE%C1%F1%FD%E0%F7%B0%A8%B0%C2%E7%F7%F6%F7%B2%F5%E7%F3%E0%F6%F3%E0%B2%FE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%E6%F3%FC%E6%F3%E1%B2%E4%F7%F1%F7%E1%B2%F1%FD%FF%FD%B2%E3%E7%FB%F7%E0%F3%B0%BE%B0%FF%E1%F5%CB%FD%E7%DE%F3%E1%E6%C1%F1%FD%E0%F7%B0%A8%B0%DE%F3%B2h%FE%E6%FB%FF%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%F5%E7%F3%E0%F6%F3%F6%F3%B2%F7%E1%B0%BE%B0%FF%E1%F5%D3%F1%E6%FB%E6%EB%D1%FD%FF%E2%FE%EB%B0%A8%B0%CB%F3%B2%FA%F3%B2%E0%F7%F3%FE%FB%E8%F3%F6%FD%B2%F7%E1%E6%F3%B2%F3%F1%E6%FB%E4%FB%F6%F3%F6%BC%B0%BE%B0%FF%E1%F5%C2%FE%F3%EB%C1%F7%E4%F7%E0%F3%FE%C6%FB%FF%F7%E1%B0%A8%B0%C2%E7%F7%F6%F7%B2%E0%F7%F3%FE%FB%E8%F3%E0%B2%F7%E1%E6%F3%B2%F3%F1%E6%FB%E4%FB%F6%F3%F6%B2%F1%E7%F3%FC%E6%F3%E1%B2%E4%F7%F1%F7%E1%B2%E3%E7%FB%F7%E0%F3%B0%BE%B0%FF%E1%F5%D4%E7%FE%FE%C1%F1%E0%F7%F7%FC%B0%A8%B0%C2%F3%FC%E6%F3%FE%FE%F3%B2%D1%FD%FF%E2%FE%F7%E6%F3%B0%BE%B0%FF%E1%F5%D7%EA%FB%E6%D4%E7%FE%FE%C1%F1%E0%F7%F7%FC%B0%A8%B0%C1%F3%FE%FB%E0%B2%F6%F7%FE%B2%FF%FD%F6%FD%B2%E2%F3%FC%E6%F3%FE%FE%F3%B2%F1%FD%FF%E2%FE%F7%E6%F3%B0%BE%B0%FF%E1%F5%DF%FD%E4%F7%DD%FC%F7%B0%A8%B0%C2%F3%E1%F3%E0%B0%BE%B0%FF%E1%F5%D3%E7%F6%FB%FD%B0%A8%B0%D3%E7%F6%FB%FD%B0%EF%EF
0123456789101112131415161718192021222324252601234567891011121314151617181920212223242526
Su navegador no es compatible con esta herramienta.

Opción B: Cada gráfica con su coeficiente




Opción C: ¿Verdad o mentira?

Indicar si son verdaderas o falsas las siguientes afirmaciones.

Pregunta 1

Dadas dos variables cualesquiera, X e Y, el coeficiente de correlación lineal entre ellas, tiene el mismo signo que la pendiente de la recta de regresión de Y sobre X.

Pregunta 2

El coeficiente de correlación lineal de una distribución bidimensional es -1,5.

Pregunta 3

Si el coeficiente de correlación lineal entre dos variables, X e Y, vale 0,5; el coeficiente de correlación lineal entre las variables Y y X vale 1/0,5.

Pregunta 4

La pendiente de las rectas de regresión de Y sobre X y de X sobre Y, es del mismo signo.

Pregunta 5

Se sabe que entre el consumo de papel de los habitantes de una ciudad, y su consumo de agua, no existe ninguna relación, por tanto, la covarianza es -1.

Pregunta 6

Si dos variables son incorreladas, sus rectas de regresión son paralelas.

Opción D: En regresión

Para los siguientes ejercicios, calcula las rectas de regresión. Compara los resultados con tu compañero.

  1. EL consumo de energía “per cápita” en miles de kw/h y la renta “per cápita” en miles de euros de seis países de la UE son las siguientes:  La imagen muestra la tabla del enunciado del problema
  2. En una muestra de 64 familias se ha estudiado el número de miembros en edad laboral, X, y el número de ellos que están en activo, Y. Los resultados se recogen en la tabla siguiente: La imagen muestra una tabla con los datos del enunciado del problema
  3. Una empresa desea conocer la relación existente entre el número de horas trabajadas y los salarios percibidos por sus empleados. En la tabla se presenta el número de trabajadores en cada categoría de horas semanales trabajadas y salario mensual (en decenas de €) percibido.

La imagen muestra una tabla con los datos del enunciado del problema

5. Reviso lo que aprendo

Reflexiona un momento sobre todo lo que has aprendido hasta llegar aquí. 

Y completa el PASO 3 de tu Diario de Aprendizaje (Reviso lo aprendido). 

Recuerda:

  • Pregunta a tu profesor o profesora si la rellenarás en papel o en el ordenador.
  • Si la rellenas en el ordenador, ¡no te olvides de guardarla en tu ordenador cuando la termines!

¡Ánimo, que lo harás genial!

Motus dice... ¿Te has dado cuenta de la cantidad de cosas que has tenido que hacer para completar cada una de las actividades?

Al realizar estas actividades, como por ejemplo la actividad “El rosco bidimensional”, has tenido que poner en juego todo lo que sabes. A veces para aprender tenemos que trabajar de forma constante. Cuando nos esforzamos mucho, nuestro trabajo es valorado por nuestros profes y familiares. Pero lo más importante es que nos sentimos muy contentos por el trabajo realizado.

Te animo a que sigas trabajando para que puedas aprender y seguir mejorando.

Creado con eXeLearning (Ventana nueva)