Diccionario
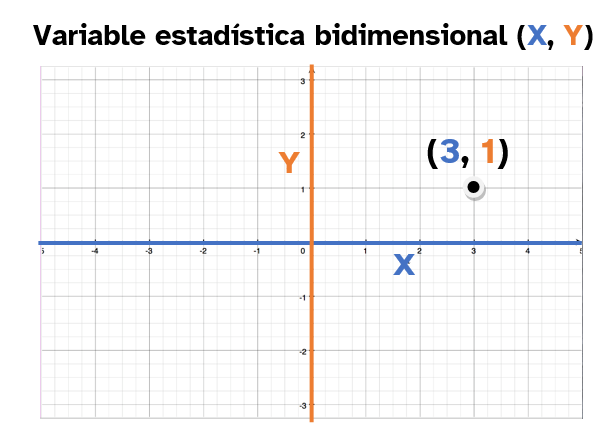
Ejes cartesianos
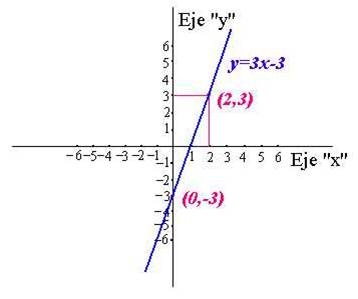
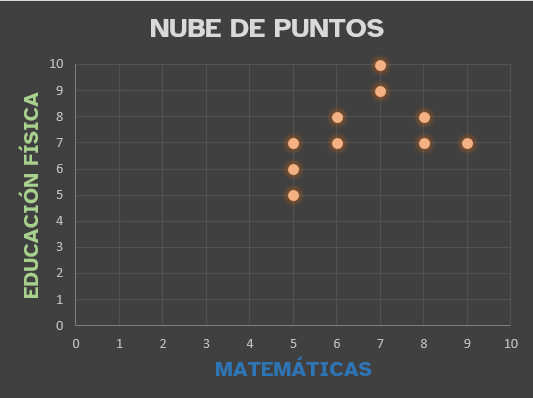
Gráficas

Ahora que ya sabes de la importancia de las variables estadísticas bidimensionales y de la utilidad de las tablas para recoger la información.
Ha llegado el momento de representar las variables en el plano y de estudiar la relación que existe entre las variables.
Las gráficas te serán muy útiles para ver si las variables de tu estudio final están relacionadas o no.
De nuevo cuentas con la ayuda de Ajustino y Ajustina con los que te entrenarás en las representaciones de variables.
¡Adelante con la representación!
 Definición:
Definición:
Representación de datos numéricos a través de recursos visuales.Representación de datos numéricos a través de recursos visuales.
Ejemplo:El profesor nos mandó hacer una gráfica con los datos de las precipitaciones de los meses de otoño.
Lectura facilitada
Ya sabes la importancia de las variables estadísticas bidimensionales y
la utilidad de las tablas para recoger la información.
Ahora vas a representar las variables en el plano y
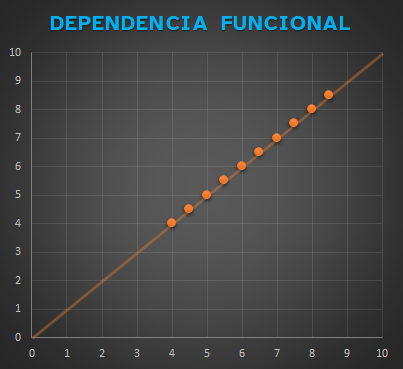
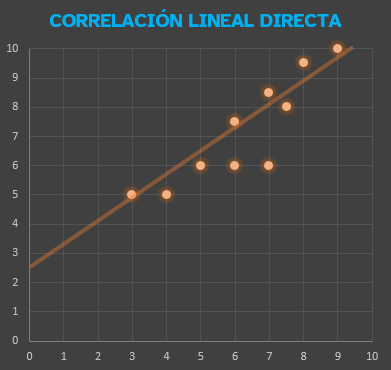
vas a estudiar la relación que existe entre las variables.
Las gráficas son útiles para ver si las variables de tu estudio final
están relacionadas o no.
Ajustino y Ajustina te van a ayudar en las representaciones de variables.
¡Adelante con la representación!

Representación de datos numéricos a través de recursos visuales.Representación de datos numéricos a través de recursos visuales.
Ejemplo:El profesor nos mandó hacer una gráfica con los datos de las precipitaciones de los meses de otoño.