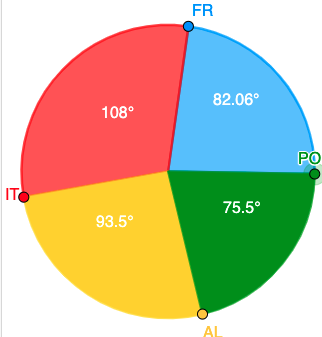
Diccionario
Expresión Algebraica
- Definición
-
Es una combinación de letras y números relacionadas por operaciones matemáticas: suma, resta, multiplicación y división. A las letras les llamamos incógnitas porque no sabemos su valor.
- Ejemplo
-
3x o x-7
Ecuación
- Definición
-
Una ecuación son dos expresiones algebraicas separadas por el signo igual (=). Las incógnitas de una ecuación tienen un valor concreto que tienes que averiguar.
- Ejemplo
-
2x-5=8x
Directamente proporcional
- Definición
-
Dos cantidades son proporcionales cuando una de las cantidades al hacerse más grande o más pequeño, la otra cantidad lo hace en la misma proporción.
- Ejemplo
-
La frecuencia absoluta de un valor de la variable es 4 y el ángulo que le corresponde es 20º, entonces si la frecuencia absoluta de otro valor es 8, el ángulo que le corresponde es 40º.
Proporcional
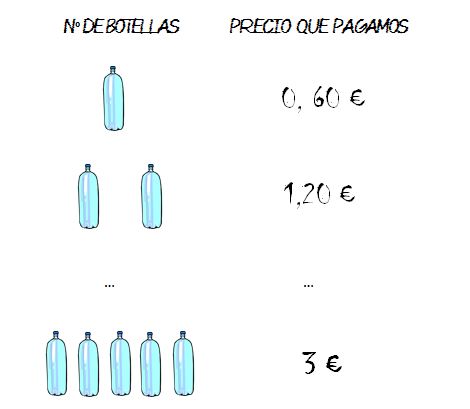
- Definición
-
Es la relación que existe entre dos magnitudes como el peso o la longitud cuando tienen una proporción o razón constante, es decir, el resultado de dividir dos valores relacionados es siempre el mismo.
- Ejemplo
-
1 botella vale 0,60 €.
0,60=0,60*1
2 botellas valen 1,20 €.
1,20=0,60*2
5 botellas valen 3 €.
3=0,60*5
El precio es proporcional al número de botellas.
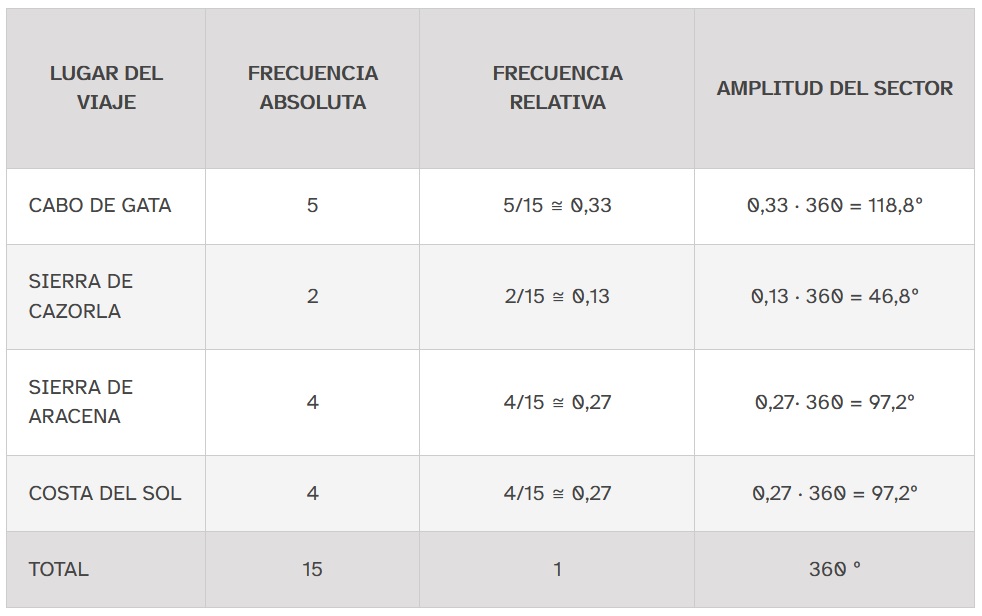

 ¡Anímate a elegir más de una de las siguientes opciones de esta actividad! En cada una de ellas descubrirás las características y la utilidad de los diagramas de sectores para representar datos de una encuesta.
¡Anímate a elegir más de una de las siguientes opciones de esta actividad! En cada una de ellas descubrirás las características y la utilidad de los diagramas de sectores para representar datos de una encuesta.