¿Necesitas recordar qué es un Histograma?
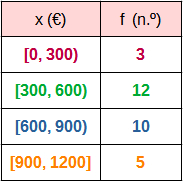
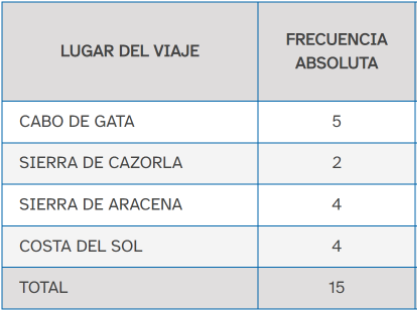
En el apartado anterior has visto un tipo de representación gráfica de datos estadísticos: el diagrama de barras. Es apropiado para el caso de variable cualitativa, como el ejemplo que puedes ver en la figura: la tabla de lo que prefieren los 15 alumnos de una clase en cuanto a la localidad de destino del viaje.
Si ahora quisieras representar las cantidades de dinero que se pueden gastar, es probable que no hubiesen muchas coincidencias, y en el diagrama quedarían muchas barras y además de alturas casi iguales.
Por ello, tenemos que agrupar los valores de la variable en intervalos y realizar un “histograma''. Esto es lo que va a suceder cuando trabajamos con variables cuantitativas continuas.
Un histograma es un gráfico parecido al diagrama de barras, pero con las barras pegadas una tras otra, de forma que cada una comienza exactamente donde termina la anterior.
Puesto que trabajamos con datos agrupados en intervalos, tomaremos como base la anchura del intervalo que estemos utilizando. Esa anchura es el resultado de la resta entre los extremos del intervalo.
Si todos los intervalos tienen la misma anchura, la altura será entonces proporcional a la frecuencia de cada uno. Lo más habitual es que la altura sea exactamente el mismo número que la frecuencia.
Easier to read
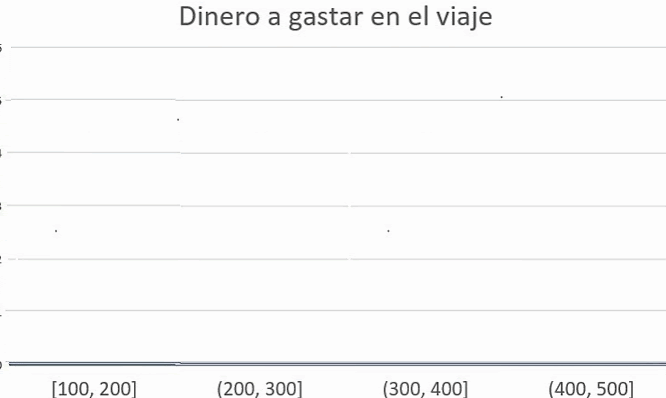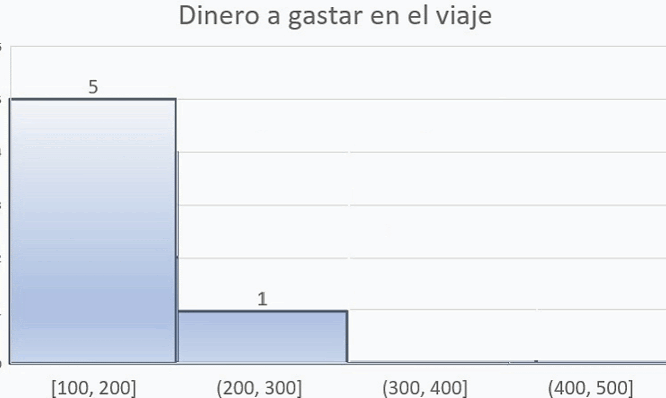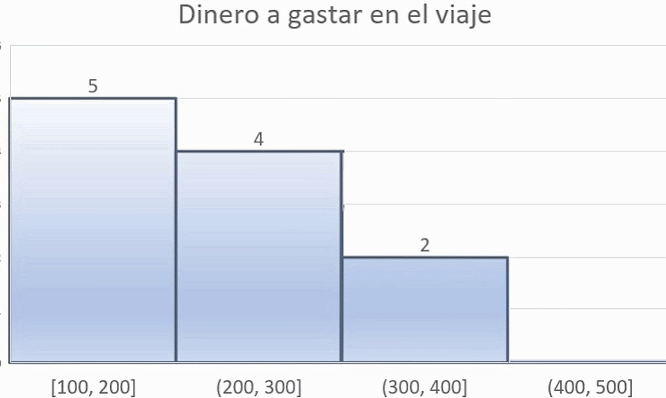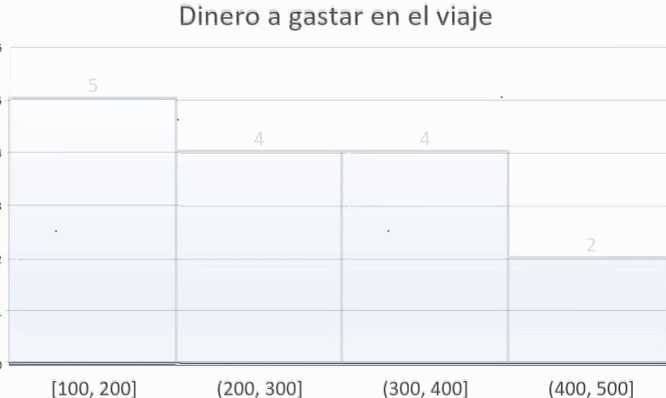
Para representar la cantidad de dinero a gastar usamos el histograma.
El histograma es un gráfico parecido al diagrama de barras.
Para realizar un histograma
tienes que agrupar los valores de la variable en intervalos.
El histograma se usa para representar las variables cuantitativas continuas.
Por ejemplo: La cantidad de dinero que quieres gastar para el viaje.
En el eje de coordenadas X del histograma se escribe el intervalo.
En el eje de coordenadas Y se dibujan las barras.
Las barras tienen una altura proporcional a la amplitud de cada intervalo.
Por ejemplo:
| DINERO A GASTAR |
MARCA DE CLASE |
FRECUENCIA ABSOLUTA |
| [100,200) | 150€ | 5 |
|
[200,300) |
250€ |
2 |
|
[300,400) |
350€ |
4 |
| [400,500) | 450€ | 4 |
TOTAL |
SUMA TOTAL= 15 |
|
¡Anímate a elegir más de una de las siguientes opciones de esta actividad! En cada una de ellas descubrirás las características y la utilidad de los histogramas para representar datos de una encuesta. 
