Diccionario
Azar
Conglomerado
Estratos
Muestra
.jpg)
Definición:
Llamamos muestra a una parte de la población.
Ejemplo:
Para realizar el estudio se utilizó una muestra de 8 estudiantes.
Muestreo aleatorio
Tamaño de la muestra
Detectives Estadísticos
4.2. Preguntando al azar
Hay veces en las que no es posible preguntar a todo el mundo por falta de tiempo, dinero o de otros elementos.
Por ello, tenemos que buscar una forma de hacerlo que esté en nuestras manos. ¿Quieres conocer cómo se hace?
1. Muestra
Recuerda cuando hablamos del Viaje de Estudios y preguntamos a dónde queríais ir. Como en tu clase hay pocos estudiantes, no habría problema en preguntar a todos pero ¿qué sucedería si hay que hacerlo en todo el centro?
En ese caso habría que preguntar a muchas personas y tardaríamos mucho, por lo que podría ser interesante preguntar sólo a unas pocas.
Cuando elegimos solo a una parte de la población para hacer una encuesta, estamos tomando una muestra.
Recuerda cuando preguntamos solo a las personas portavoces de los grupos sobre el destino del viaje. Acabamos el estudio muy pronto pero no teníamos la opinión de todo el mundo. ¿Recuerdas que pasó entonces? ¿Coincidió tu opinión con la de tu portavoz? ¿Y la de la mayoría de los miembros del grupo?
Como pudiste comprobar, las muestras nos ayudan a hacer nuestro estudio estadístico más rápido, pero no tenemos la misma información que sí preguntáramos a todo el mundo. Por tanto, debes elegir la muestra siguiendo las indicaciones que te damos para que los resultados sean correctos.
Definición
Llamamos muestra a una parte de la población.
Ejemplo
Para realizar el estudio se utilizó una muestra de 8 estudiantes.
Lectura facilitada
Recuerda cuando hablaste del viaje de estudios y se preguntó:
¿Dónde queréis ir?
Para saber la respuesta tienes que preguntar a los compañeros y compañeras.
Hay muchos compañeros y compañeras en el instituto para preguntar.
Por este motivo eliges un grupo pequeño de chicos y chicas de tu instituto para preguntar.
La muestra es el grupo pequeño de personas que eliges para preguntar.
Por ejemplo: Eliges a los compañeros y compañeras de tu clase
para hacer la pregunta de ¿Dónde queréis ir de viaje?
El grupo de compañeros y compañeras de tu clase son la muestra.
Debes elegir la muestra adecuada para que los resultados sean
correctos.
2. Definiciones y tipos de muestreo
Cuando preguntamos a los portavoces, éstos forman la muestra.
Una parte de la población se llama muestra.
El número de individuos que la componen se llama tamaño de la muestra.
Uno de los principales problemas a la hora de tomar una muestra es cómo elegirla. ¿Recuerdas cómo la hiciste?
La forma más habitual es elegir a una persona al azar. En ese caso, se llama muestreo aleatorio.
Definición
Es el número de individuos que componen la muestra.
Ejemplo
La muestra tiene 8 sujetos.
Definición
Forma habitual de elegir personas al azar.
Ejemplo
La muestra se elegirá cuando se realice el sorteo de 5 números entre los 20 alumnos.
Lectura facilitada
Cuando preguntas a los portavoces de cada grupo estás cogiendo una muestra.
La muestra es el grupo de personas que eliges para preguntar.
El tamaño de la muestra es el número de personas que eliges para preguntar.
Por ejemplo: Cada grupo tiene un portavoz. Hay 5 portavoces.
El tamaño de la muestra es de 5 personas.
-------------------------------------------------------------------------------------------------------------------
¿Cómo eliges a las personas que quieres preguntar?
Para elegir a las personas que quieres preguntar puedes hacerlo al azar.
Elegir al azar es cuando eliges a las personas
por casualidad y no por una razón.
Por ejemplo: Cuando coges la lista de tu clase
y pones tu dedo encima de un nombre sin mirar.
El nombre que señalas ha sido al azar.
El muestreo aleatorio es cuando eliges un grupo de personas al azar
para preguntar.
Definición:
Elegir al azar es cuando eliges a las personas por casualidad y no por una razón.
Por ejemplo:
Cuando coges la lista de tu clase y pones tu dedo encima de un nombre sin mirar. El nombre que señalas ha sido al azar.
3. Calcula aquí el tamaño de la muestra
En este applet de Geogebra puedes calcular el tamaño de la muestra.
Puedes investigar qué sucede al cambiar los errores y los niveles de confianza.
4. Nuestro primer muestreo
Imagina que quieres saber el destino favorito de viaje de tus compañeros y compañeras de clase. Y debes saberlo en un minuto para poder hacer una oferta de viaje.
¿Qué harías?
- ¿Preguntas a todos tus compañeros y compañeras? o ¿Eliges una muestra?
- ¿Cómo eliges a las personas para la muestra?
- ¿Por qué?
- ¿De qué tamaño sería la muestra?
- ¿Merece la pena el proceso de tomar una muestra?
- ¿Y si son todos los alumnos de tercero de ESO?
Piensa en las respuestas de estas preguntas, coméntalas con tu compañero y exponlas en clase.
Lumen dice ¿Pensabas que en una encuesta tienes que preguntar a todo el mundo?
¡Fíjate que con un poco de planificación podemos conocer muchas cosas sin necesidad de hablar con todos!
5. Otros tipos de muestreo
Aparte de la anterior, existen diversas formas de elegir una muestra:
Muestreo estratificado.
En este tipo de muestreo, hacemos estratos (grupos) dentro de una población y luego elegimos individuos dentro de cada estrato. Estos estratos pueden ser homogéneos o heterogéneos.
Muestreo aleatorio sistemático
En este tipo de muestreo, primero ordenamos la población con el criterio que queramos, después elegimos un individuo y, a partir de él, elegimos los demás individuos que forman la muestra.
Por ejemplo, si tenemos 100 individuos ordenados, elegimos al primero y tomamos los demás elementos de la muestra de 5 en 5, de 10 en 10, dependiendo del tamaño que queramos dar a la muestra.
Muestreo por conglomerados
En este tipo de muestreo, dividimos la población en grupos “naturales”, por ejemplo, clases del centro, barrios de una localidad, provincias de España. Luego, elegimos uno de esos conglomerados para realizar nuestro estudio.
Definición
Es un grupo de personas que están ubicadas en un mismo lugar donde comparten cosas similares como religión, gustos y estilos de vida.
Ejemplo
Las clases sociales son estratos de la población.
Definición
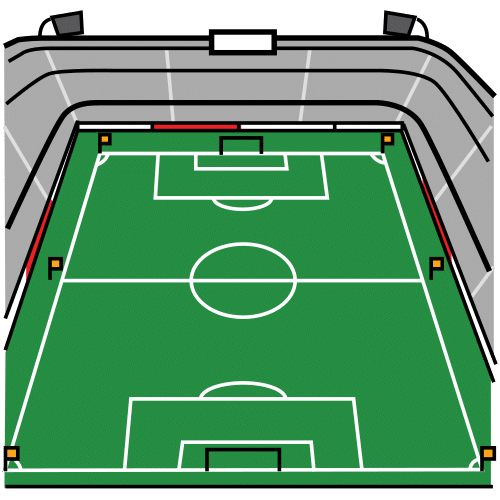
Son grupos de personas con un fin en común, pero sin comunicación entre ellas y sin interactuar entre sí.
Ejemplo
Un estadio de fútbol es un conglomerado, donde miles de personas van a ver a su equipo favorito, pero no se comunican entre ellas.
Definición
Es un grupo de personas que están ubicadas en un mismo lugar donde comparten cosas similares como religión, gustos y estilos de vida.
Ejemplo
Las clases sociales son estratos de la población.
Lectura facilitada
Muestreo estratificado
En el muestreo estratificado haces grupo de personas y luego
eliges a una persona de cada grupo
Los grupos pueden ser homogéneos y heterogéneos.
Grupos homogéneos: todas las personas que forman el grupo son iguales.
Grupos heterogéneos: las personas que forman el grupo son distintas.
Muestreo aleatorio sistemático
Es cuando:
1. Ordena a las personas.
2. Elige al azar una persona.
3. Después, elige la cantidad que vas a sumar de forma fija.
4. Las demás personas se eligen sumando la cantidad fija que has elegido.
Por ejemplo:
Tienes 100 personas ordenadas.
Eliges una persona al azar del grupo. Por ejemplo: el 3.
Decide la cantidad fija. Por ejemplo: 5.
Para elegir al resto de personas
tienes que sumar de 5 en 5 desde el número 3: 3, 8, 13...
Muestreo por conglomerados
Divide la población en grupos.
Por ejemplo:
Clases del centro.
Barrios de la ciudad.
Provincias de España.
Elige uno de esos grupos para realizar tu estudio
6. Dos números importantes
Tomar una muestra nos facilita mucho realizar un estudio estadístico.
Pero esta ventaja tiene un riesgo, ya que cada vez que tomamos una muestra, puede ser que los datos que obtengamos tras estudiarla no sean los que hubiéramos obtenido al estudiar la población.
Por ello, a la hora de elegir una muestra hay dos valores muy importantes que tenemos que fijar, según el riesgo que queramos correr.
Error del muestreo
Es la probabilidad de que la muestra sea diferente a la población..
Por tanto, a la hora de determinar el tamaño de la muestra debemos especificar qué error máximo estamos dispuestos a admitir.
Habitualmente ese error que se asume es de 0.05 (el 5%).
Cuanto más grande sea el error que asumamos más pequeña será la muestra a tomar.
Cuanto más pequeño sea el error que asumamos más grande será la muestra a tomar.
Nivel de confianza
Es la probabilidad de que los parámetros estadísticos de la muestra sean parecidos a los de la población.
Hay distintos valores para el nivel de confianza dependiendo de la necesidad que tengamos de obtener unos resultados parecidos a los de la población.
El más habitual es 1.96.
Cuanto más grande sea el nivel de confianza que queramos tener más grande tendrá que ser la muestra.
Cuanto más pequeño sea el nivel de confianza que queramos tener más pequeña tendrá que ser la muestra.
Lectura facilitada
La muestra ayuda a realizar un estudio estadístico.
Pero a veces los datos que obtenemos de la muestra es diferente
a los datos de la población.
Para elegir una muestra tienes que fijarte en:
Error en el muestreo
El error del muestreo es la posibilidad de que nuestra muestra tenga
resultados diferentes a la población.
Cuando eliges el tamaño de la muestra debes decidir qué error máximo va a tener.
El error que se admite suele ser 0,05. 0,05 es un 5%.
Cuando el error es más grande,
la muestra que elegimos debe ser más pequeña.
Cuando el error es más pequeño,
la muestra que elegimos debe ser más grande.
Nivel de confianza
El nivel de confianza es la posibilidad de que nuestra muestra tenga
parámetros estadísticos parecidos a la población.
El nivel de confianza más usado es 1,96.
Cuando el nivel de confianza es más grande,
la muestra que elegimos debe ser más grande.
Cuando el nivel de confianza es más pequeño,
la muestra que elegimos debe ser más pequeña.
Puedes calcular el tamaño de una muestra con el siguiente Geogebra.
Obra publicada con Licencia Creative Commons Reconocimiento Compartir igual 4.0