Diccionario
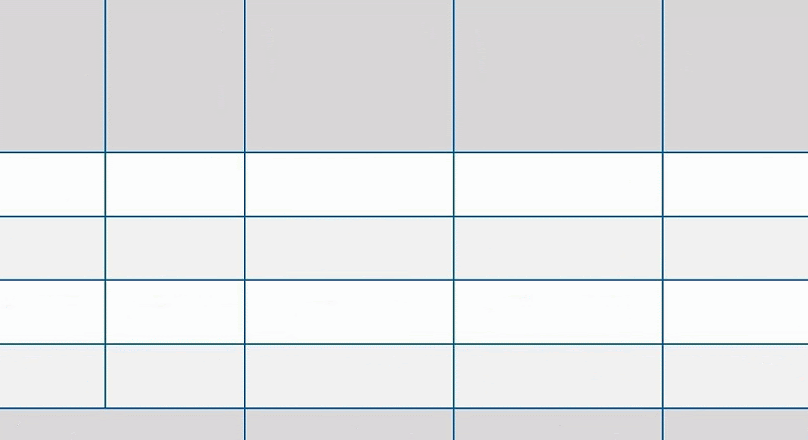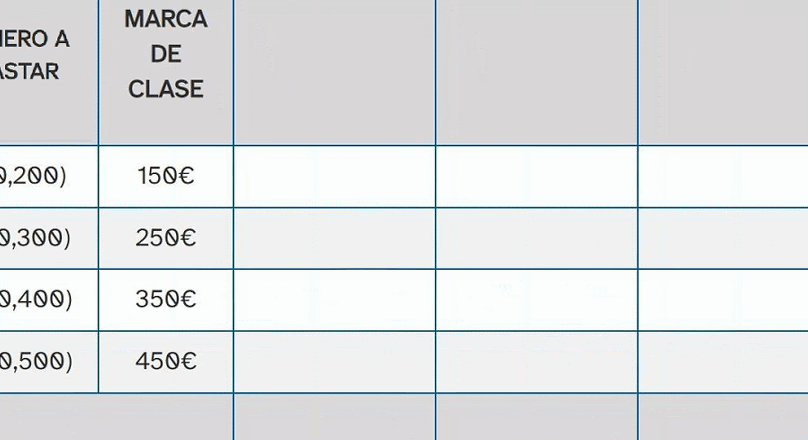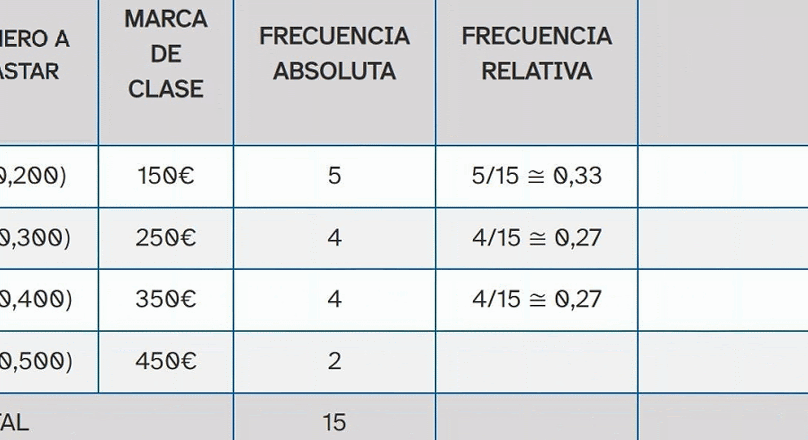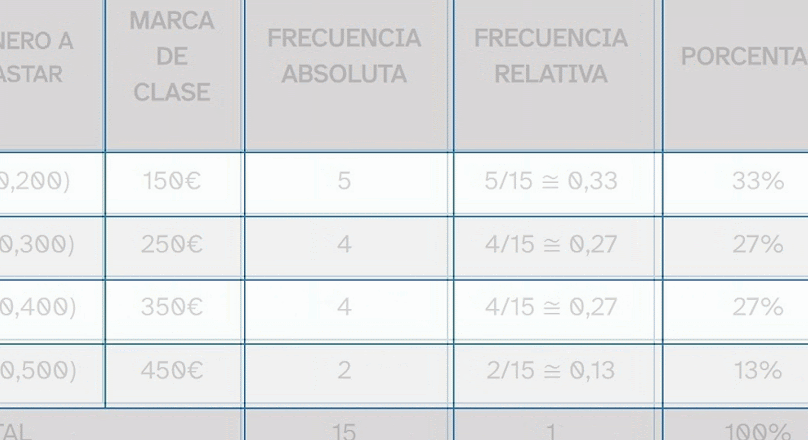
Frecuencia Absoluta

- Definición
-
Número de veces que aparece un valor. De ahora en adelante, representaremos la frecuencia absoluta por : \(n_{i}\)
- Ejemplo
-
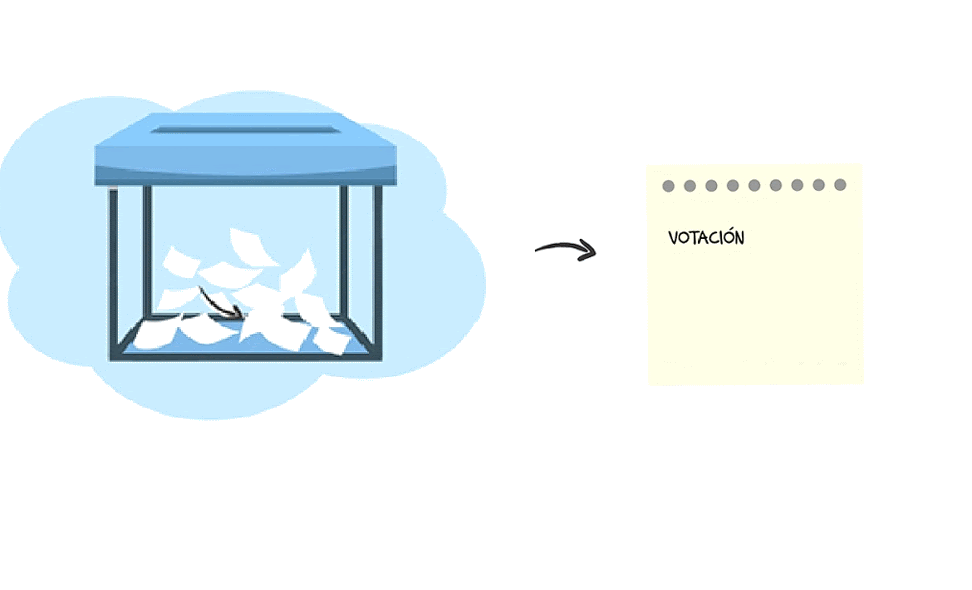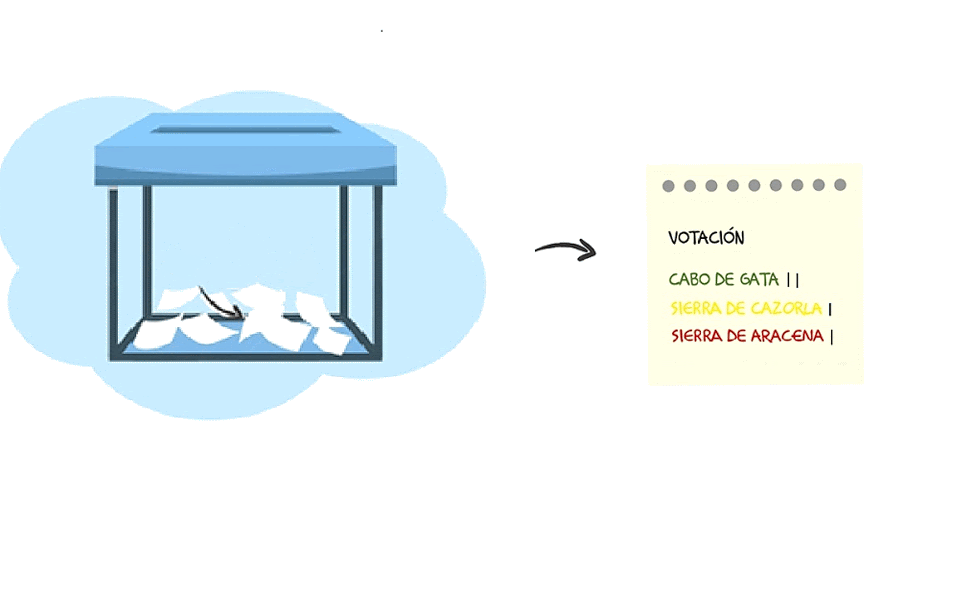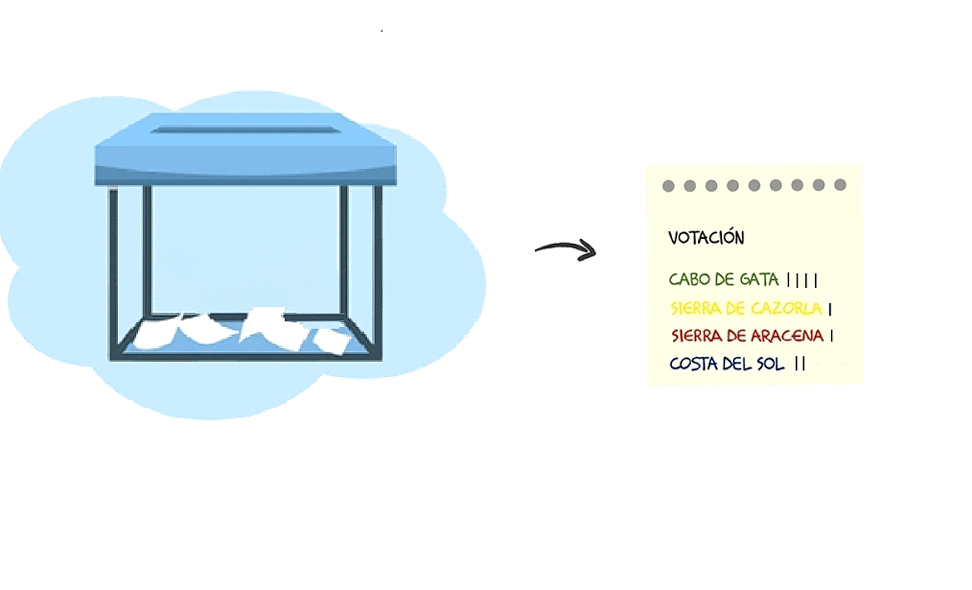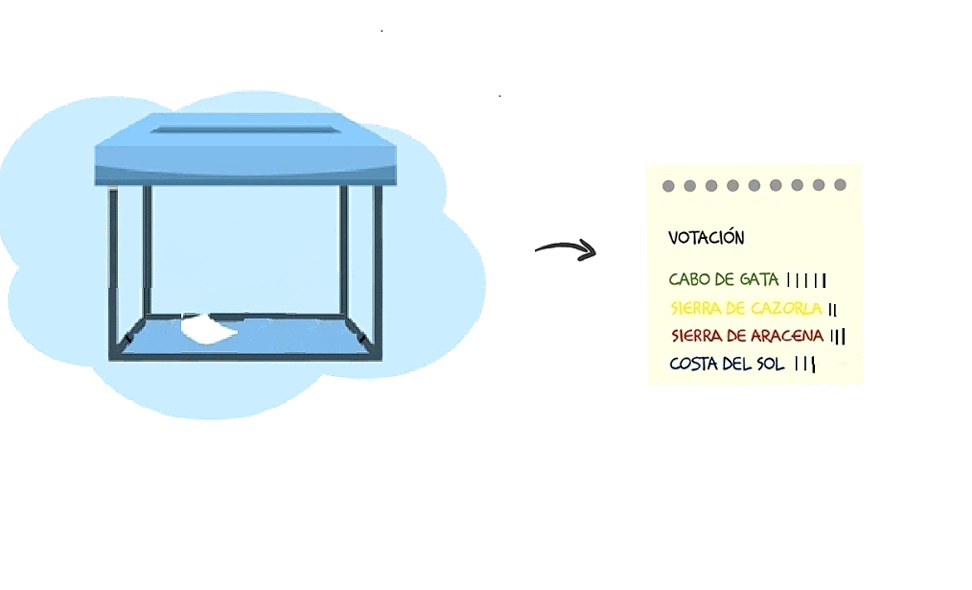
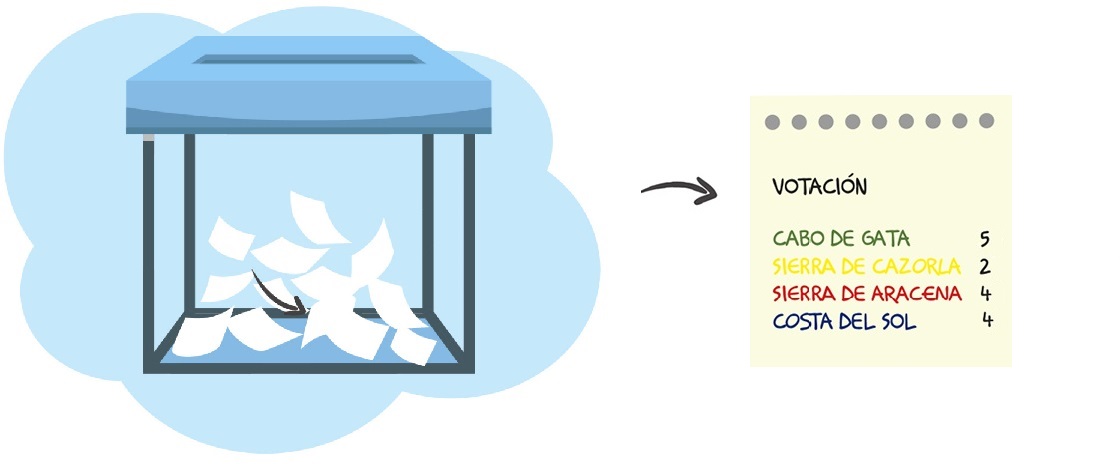
La frecuencia absoluta es el número de votos que ha tenido cada destino.
Frecuencia Relativa
- Definición
-
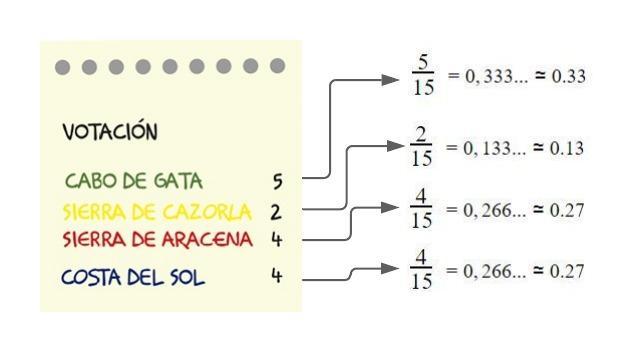
Cociente entre la frecuencia absoluta de un valor y el número total de datos. De ahora en adelante, representaremos la frecuencia absoluta por : \(f_{i}\)
- Ejemplo
-
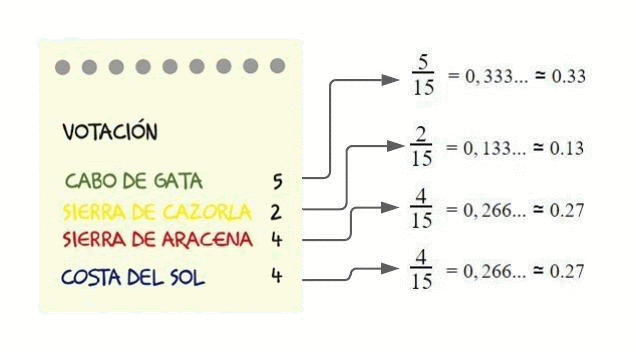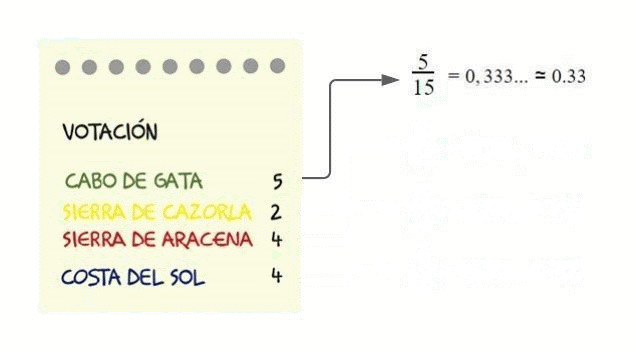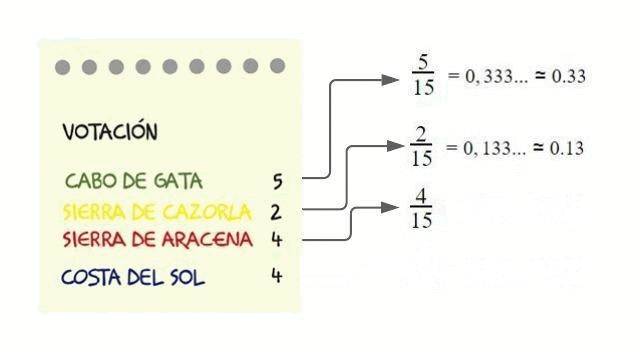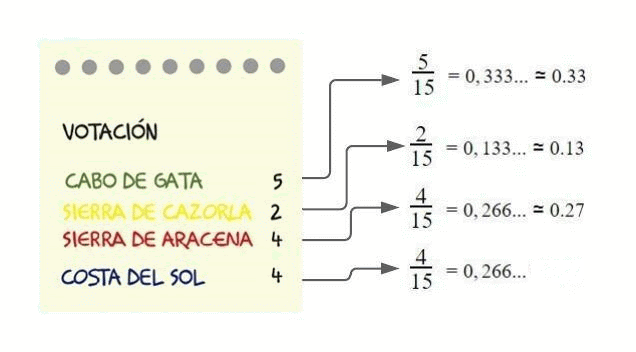
El número total de votos para elegir destino ha sido de 15 votos. Cabo de Gata ha recibido 5 votos. El resultado de 5 dividido entre 15 es la frecuencia relativa.
Intervalos
- Definición
-
Parte de tiempo o de espacio que hay entre dos hechos o dos cosas.
- Ejemplo
-
En el intervalo entre 20 y 30 años, el número de personas varía de 8 a 10.
Porcentaje
- Definición
-
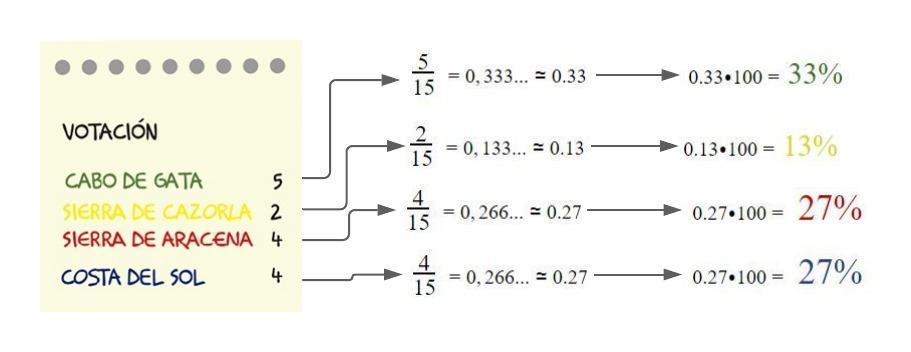
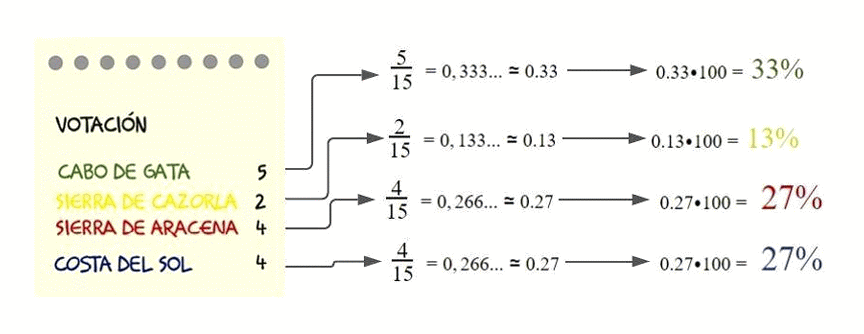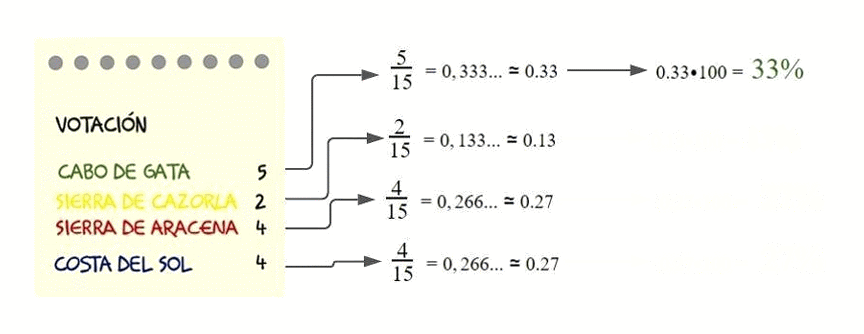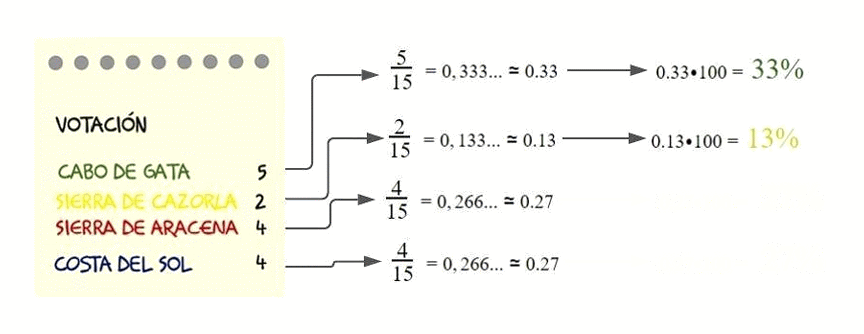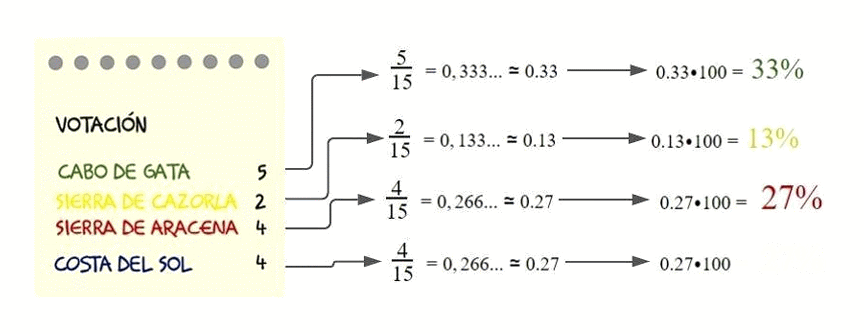
Número que representa una cantidad sobre un total de 100. Su símbolo es %
- Ejemplo
-
El porcentaje de personas con discapacidad en España es del 10 por ciento. Esto significa que hay 10 personas con discapacidad por cada 100 personas en España
Tabla estadística
- Definición
-
Es una tabla en la que ordenamos los valores y frecuencias que toma una variable estadística.
- Ejemplo
-
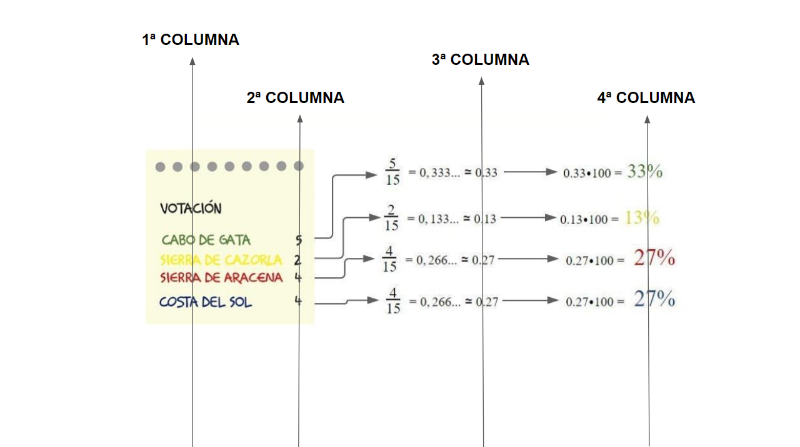
Esta tabla estadística tiene dos columnas.
Votos
- Definición
-
El voto es el acto por el cual una persona expresa su apoyo a una causa para tomar decisiones.
- Ejemplo
-
La clase votó el destino del viaje de fin de curso.
 ¿Recuerdas cuando preguntamos por dónde queríamos ir de viaje?
¿Recuerdas cuando preguntamos por dónde queríamos ir de viaje?